科技工作者之家
科技工作者之家APP是专注科技人才,知识分享与人才交流的服务平台。
科技工作者之家 2020-11-17
阿达马三圆定理是一个关于全纯函数性质的结论。即:设f(z)是环域 上的全纯函数,M(r)是|f(z)|在圆周|z|=r上的最大值。那么,logM(r)是一个对数log(r)的凸函数。
简介阿达马三圆定理是关于圆环内解析函数在圆环的同心圆周上的最大模的增长性定理。1
定义设 f(z) 是环域 上的全纯函数, M(r) 是 | f(z) | 在圆周 | z | = r 上的最大值。那么, logM(r) 是一个对数 log(r) 的凸函数。进一步,如果不存在常数 λ 和c,使得 f(z) 是 cz 的形式,那么 logM(r) 是 log(r) 的严格凸函数。
定理结论可以重述为:
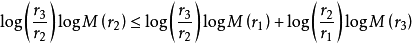
对任何半径为 r1 推导
阿达马三圆定理 在复分析中,阿达马三圆定理是一 个关于全纯函数性质的结论。 设 f(z) 是环域 上的全纯函 数, M(r) 是 | f(z) | 在圆周 | z | = r 上的最大值。那么, logM(r) 是 一个对数 log(r) 的凸函数。 进一步, 如果不存在常数 λ 和 c,使得 f(z) 是 cz 的形式,那么 logM(r) 是 log(r) 的严格凸函数。
定理结论可以重述为: 对任何半径为r1