自配极四面形学术资讯 - 科技工作者之家

自配极四面形(self-polarity tetrahedron)亦称自配极四面体，是关于二阶曲面∑的特殊四面体。在射影空间中，若一个四面形的每个顶点都是其对面关于∑的极点，则这个四面形称为自配极四面形1。

基本概念通过二次曲面外一点P的直线与曲面相交于X,Y两点，如果关于X,Y，点P的调和共轭点为Q，则点Q的轨迹是平面。这个平面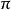称为关于二次曲面的点P的极面(polarplane)，点P称为这个平面π的极点或极(pole)。当点P的极面通过点Q时，点Q的极面通过点P，这时称P,Q两点对于二次曲面是共轭的(conjugate)。当P点在二次曲面上时，可以认为极面是在P点的切平面。关于无奇点的二次曲面，当四面形各顶点的极面是对应于它的顶点的平面时，这个四面形称为自配极四面形(selfpolar tetrahedron)。四面形A的四个顶点的关于二次曲面的极面为四面形B的平面时，交换A,B后也有同样的性质。这样的两个四面形，称为关于二次曲面互为配极四面形(polartetrahedron)。关于二次曲面，当两个平面中一个平面的极点在另一个平面上时，称这两个平面关于二次曲面是共轭的(conjugate)。

当两个平面束有射影关系时，其对应的二平面交线的轨迹一般是单叶双曲面或双曲抛物面。特别是当平面束的轴相交时，这个轨迹是二次锥面，轴互相平行时为二次柱面(即椭圆柱面或双曲柱面)，当考虑不在同一平面上的二直线的射影对应时，通过其对应点的直线的轨迹也成为二次曲面(M.Chasles)2。

相关介绍设r,s是任意一直径p的共轭平面π与曲面的交线K的任意一对共轭直径，则[p,r]，[p,s]是曲面的一对共轭直径平面。

因r,s是任意的，且属于同一对合，故通过p有无限对共轭直径平面，且也属于同一对合;这个对合的固定元素是曲面通过P的二切面。

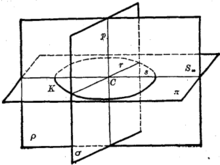
设C是一二次曲面的中心，则一般可以引一个而且只有一个平面π通过C且共轭于p，π称为p的一个共轭直径平面，或称p为π的一条共轭直线。所以，对于一个有心二次曲面的任一直径p必存在一个共轭直径平面与它对应，这个平面π的极点就是p的象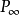，其次，在π上取其与曲面相交的曲线K的任意两条共轭直径r,s，于是得到三个平面[r,s]≡π,[p,s]≡ρ,[p,r]=σ,其中任二平面是共轭平面，因而这三个平面构成一个自配极三面形，它与t=0构成一个自配极四面体、自配极三面形的三条棱称为二次曲面的三条共轭直径、由这个作图法就可以知道，通过中心C存在无限组共轭平面p,σ,π3。