德卡斯特里奥算法

数学子领域数值分析中的德卡斯特里奥算法（De Casteljau's algorithm），以发明者保尔·德·卡斯特里奥命名，是计算伯恩斯坦形式的多项式或贝济埃曲线的递归方法。虽然对于大部分的体系结构，该算法和直接方法相比较慢，但它在数值上更为稳定。1

定义贝兹曲线B（角度为n，控制点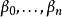）可用以下方式运用德卡斯特里奥算法：

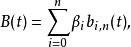其中，b为伯恩施坦基本多项式。

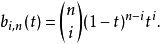曲线在t0点上可以用递推关系式运算。

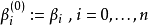
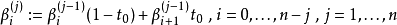
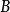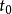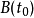然后，在点上的计算可以此算法的 步计算。 的结果为：

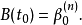再者，贝兹曲线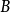可在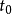分成带有各种控制点的两段曲线：

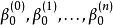
注意事项进行手算时把系数写成三角形形式很有用。

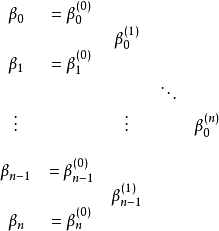当选择一点t0来计算波恩斯坦多项式时，我们可以用三角形形式的两个对角线来构造多项式的分段表示。

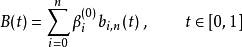把它变成

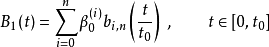以及

例子我们要计算2次波恩斯坦多项式，其伯恩斯坦系数为2

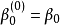
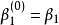
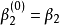
在t0点计算。

我们有下式开始递归

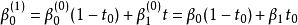
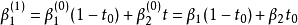
递归的第二次重复结束于

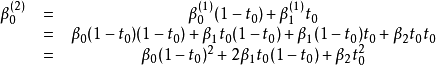
这就是我们所预料的n阶伯恩斯坦多项式。

贝塞尔曲线在计算带n+1个控制点Pi的三维空间中的n次贝塞尔曲线 (Bézier curve) 时：

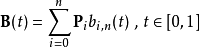其中，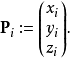

我们把Bézier曲线分成三个分立的方程：

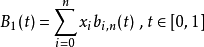
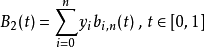
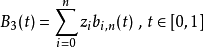
然后我们用de Casteljau算法分别计算。3

伪代码例子这是一个递归的画出一条从点P1到P4，弯向P2和P3的曲线的伪代码例子。级数参数是递归的次数。该过程用增加了的级数参数来递归的调用它自己。当级别达到最大级别这个全局变量时，在P1和P4之间就画上直线。函数中点（midpoint）去两个点，并返回这两点间的线段的中点。

global max_level = 5 procedure draw_curve(P1, P2, P3, P4, level) if (level > max_level) draw_line(P1, P4) else L1 = P1 L2 = midpoint(P1, P2) H = midpoint(P2, P3) R3 = midpoint(P3, P4) R4 = P4 L3 = midpoint(L2, H) R2 = midpoint(R3, H) L4 = midpoint(L3, R2) R1 = L4 draw_curve(L1, L2, L3, L4, level + 1) draw_curve(R1, R2, R3, R4, level + 1) end procedure draw_curve代码实现Haskell用线性插值计算P和Q之间的一点R，插值参数为t用法：linearInterp P Q t P = 代表一个点的表 Q = 代表一个点的表 t = 线性插值的参数值, t linearInterp :: [Float]->[Float]->Float->[Float]> linearInterp [] [] _ = []> linearInterp (p:ps) (q:qs) t = (1-t)*p + t*q : linearInterp ps qs t计算一对控制点间的线性插值的中间结果用法：eval t b t = 线性插值的参数值, t eval :: Float->[[Float]]->[[Float]]> eval t（bi:bj:[]）= [linearInterp bi bj t]> eval t (bi:bj:bs) = (linearInterp bi bj t) : eval t (bj:bs)用de Casteljau算法计算Bezier曲线上一点用法：deCas t b t = 线性插值的参数值, t deCas :: Float->[[Float]]->[Float]> deCas t（bi:[]）= bi> deCas t bs = deCas t (eval t bs)用de Casteljau算法计算沿着Bezier曲线的一系列点。点用一个列表返回。用法：bezierCurve n b n = 要计算的点的个数 b = Bezier控制点列表返回：Bezier曲线上n+1个点例子：bezierCurve 50 [[0,0]，[1,1]，[0,1]，[1,0]]> bezierCurve :: Int->[[Float]]->[[Float]]> bezierCurve n b = [deCas (fromIntegral x / fromIntegral n) b | x