布拉利·福尔蒂悖论

布拉利·福尔蒂悖论(Burali-Forti's paradox)亦称最大序数悖论，在集合论历史上的第一个悖论。设W为一切序数组成的集合，即W={1，2，…，ω，…}.可以看出W按自然数大小顺序成一良序集，故由W中有一序数Ω必比W中任一序数都大，但由定义知，Ω也出现在W中，从而将有Ω>Ω.而这是矛盾的。1897年3月28日在意大利巴洛摩数学会上，布拉利·福尔蒂(C.Burali-Forti)宣读了一篇论文，提出了上述悖论，揭开了数学基础第三次危机的序幕1。

基本介绍布拉利·福尔蒂悖论是关于集合的一个悖论，在古典集合论中可证如下诸命题：

1.任一良序集A不能与A的任何截段Aα相似；

2.凡由序数构成之集，按其大小为序排列时，必为一良序集；

3.由一切小于序数α的序数所组成的良序集Wα的序数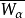 =α。

现将一切序数组成一集Γ，即Γ={x|x为一序数}，于是由命题2知，Γ可编成良序集，故有一序数γ，即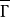 =γ，按Γ的构造知，γ∈Γ，用Γγ记Γ之元γ截Γ所获之截段，由命题3知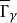， =γ，于是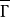 = 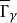，这表明Γ与其截段Γr之序数相同，因而Γ与其截段Γr相似，与命题1矛盾，这就是布拉利·福尔蒂悖论。布拉利·福尔蒂悖论被发现于1897年，实际上，德国数学家康托尔(Cantor，G.(F.P.))早在其两年前就发现了这个悖论，只是没有公开，后由意大利学者布拉利·福尔蒂(C.Burali-Forti)发现并公开之2。

背景介绍微积分的理论基础问题，由于极限论、实数论和集合论的建立而得到了解决。第二次数学危机历经两个世纪，终于排除了。人们松了一口气，于是在1900年，在巴黎召开的国际数学会议上，法国大数学家Poineare’宣称：“数学的严格性，看来今天才可以说是实现了。”事实上，当时的数学家都喜气洋洋，非常乐观。

但是这种安全的想象未能维持多久，不到两年，著名的Russell(罗素)悖论被公诸于世。Russell悖论是关于Comtor集合论的悖论，只要用逻辑术语来替代集合论术语。Russell悖论直接牵涉到逻辑理论本身，从而是直接冲击了集合论与逻辑这两门被数学家认为是最严谨的学科。这样，Russell悖论便惊动了整个西方哲学界、逻辑学界和数学界，使得许多数学家和逻辑学家不得不认真对待和研究Russell悖论问题3。

事情还得从Cantor集合论最原始的思想开始。Cantor建立古典集合论的一个最重要的思想方法就是概括原则，该原则自然、直观，使用又方便。在Cantor早期的工作中，并没有将该原则的思想明确立为公理。而只是隐蔽地被使用。直到Frege才公开而明确地把它作为公理模式使用。所谓概括原则，通俗地说，就是任给一个性质p(或概念)，我们就能把所有满足所给性质p的对象。也仅由这些具有性质p的对象汇集在一起而构成一个集合。用符号来表示就是：

G={g|p(g)} ， (1)

式中，竖线左边的g表示集合G的任一元素，而“|”右边的p(g)表示G的元素g具有性质p，又{}表示把所有具有性质p的对象g汇集成一个集合。因此，概括原则的另一表达式就是：

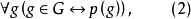亦即G的任一元素g必有性质p，而任一具有性质p的对象必为集合G的元素。

针对Cantor的集合论原始构集思想，Russell指出，有两种集合，一种是本身分子集，例如“一切概念所组成的集”，由于它本身也是一个概念，所以必为该集自身的一个元素。又如“一切集合所组成的集合”也是一个本身分子集，因为按定义知，任何集都是该集的元素，而其本身既为一集合，因而也不能例外地为该集(即其自身)的一个元素。这种集有性质x∈x，集合可以写成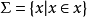 。另一种是非本身分子集，即其本身不是它自身的元素。例如，自然数集合决不是某个自然数，因此自然数集合N不可能是N的一个元素，即 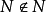，一般地写成 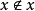，对应的集合写成 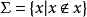。如此。任给一个集合Σ，则Σ要么是本身分子集，即Σ∈Σ，要么是非本身分子集，即 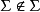。现根据Cantor的概括原则，可将一切非本身分子集汇集起来构成一集，亦即

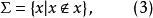此处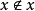 表示集合x不是它自身的元素，即x为一非本身分子集。现在要问上述一切非本身分子集( 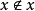)构成的集Σ是哪一种集?即问此集Σ是本身分子集，还是非本身分子集?若设Σ是本身分子集，则有Σ∈Σ，而Σ的每个元素都是非本身分子集，即性质 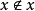，所以作为Σ之元的Σ也必须是一个非本身分子集，故 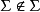。再设Σ为一非本身分子集，即 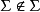，按Σ的构造知，任何非本身分子集都是Σ的元素。故Σ作为非本身分子集，亦应为Σ的一元素，即Σ∈Σ，两种说法都矛盾，都说不通。这就是著名的Russell悖论。

Russell悖论作为古典集合论中的一个悖论，不仅很快发现它可化归为最基本的逻辑概念的形式，而且进一步发现能用日常语言来表述它的基本原则，Russell自己就在1919年把它改为著名的“理发师悖论”，现陈述如下：

李家村上所有有刮胡子习惯的男人可分为两类，一类是自己给自己刮胡子的；另一类则是自己不给自己刮胡子的。李家村上有一个有刮胡子习惯的理发师自己约定：“给且只给村子里自己不给自己刮胡子的人刮胡子。”现在要问这个理发师自已是属于哪一类的人?如果说他是属于自己给自己刮胡子的一类，则按他自己的约定，他不应该给他自己刮胡子，因而是一个自己不给自己刮胡子的人。再设他是属于自己不给自己刮胡子的一类，则按他自己的约定，他必须给他自己刮胡子．因此他又是一个自己给自己刮胡子的人了。哪种说法都不通，这就是所谓“理发师悖论”。

其实在Russell悖论出现以前，古典集合论的创始者Cantor于1895年第一个在他自己所创立的集合论中发现了悖论，但他没有公开，也不敢公开。后来这个由Cantor发现的悖论由Burali-Forti发现了，并公诸于世．人们称为Burali-Forti悖论。不过当时没有引起数学家的不安，因为大家认为这只涉及到一些专门的技术问题，只要作些小修改，便能解决问题。

在Russell悖论出现后，相继出现了许多悖论，如法国人Richard于1905年提出的一个语义悖论和与其类同的一系列悖论，又如Grelling于1908年提出的一个关于形容词的悖论，直到1953年，沈有鼎先生还构造并发表了几个著名的悖论：“无根据和有根据悖论”、。循环与非循环悸沦”、“玎循环与非门循环悖论”。

在数学史上，人们把集合论悖论的出现及其所引起的争论局面，称之谓数学第三次危****机。因此，在一定程度上讲，数学第三次危机乃是前两次危机的发展和深化，因为集合论悖论涉及的问题更加深刻，涉及的范围更为广阔3。

为了排除集合论中出现的悖论，促进数学家去探索数学推理在什么情况下有效，什么情况下无效，数学命题在怎样的情况下具有真理性，在怎样的情况下失灵。于是，在本世纪初，数学基础论这一分科就诞生了。摆在从事数学基础问题研究的数学家面前的首要任务，就是如何为数学的有效性，建立可靠的依据。由于在这一工作中所持的基本观点的不同，在数学基础论的研究中形成了各个流派。其中，主要的流派有：

1)Russell的逻辑主义学派；

2)Brouwer的直觉主义学派；

3)Hilbert的Hilbert主义学派；

4)Cohen的现代形式主义学派。

以上是在数理逻辑范畴说的情况。在集合论范畴．为了排除集合论中的悖论，促使了现代公理集合论的诞生，其中最著名的有两个，即是由Bernays与Gödel建立的BG公理集合认最完善的一个系统。这些系统有一个共同点，即是在保留概括原则的“合理因素”的前提下。对造集的任意性加以适当限制。ZFC系统包括了处延、空集、配对、并集、幂集、子集(即划分)、无穷、选择、替换、正则等10条非逻辑公理。Zermelo于1908年建立了他的集合论公理系统，几经改进，最后由Fraenkel与Skolem在1921-1923年间给了一个严格的解释。进而形成著名的ZF系统，ZF系统是承认选择公理的，通常写成ZFC系统，其中英文字母C表示该系统接受选择公理。

ZFC系统的真实目的是为分析学奠定严格的基础。如前所述，微积分的基础已通过Cauchy的极限论归约到Dedekind的实数论，而实数论的不矛盾性又归约于集合论的不矛盾性。ZFC系统是以如下的路线来为微积分奠基的，这就是由无穷公理来保证自然效集的合法性，再由幂集公理导至实数集的合法化，然后再由子集公理来保证实数集中满足性质p的元所组成的子集的合法性。这样一来，只要ZFC系统无矛盾，严格的微积分理论就能在ZFC公理集合论上建立起来了。但是，问题正在于ZFC系统本身的无矛盾性至今没有被证明，所以至今不能保证在这个系统中今后不会出现悖论，虽然在ZFC系统中能够排除已经出现的那些集合论的悖论，并且ZFC系统应用到今天，尚未出现过其他矛盾。但是。Poincaré指出：我们设置栅栏．把羊群围住，免受狼的侵袭，但是很可能在围栅栏时就已经有一条狼被围在其中了。

由于ZFC系统不能保证在这个系统中今后不会出现悖论，从这个意义上来说，第三次数学危机并没有彻底解决，我们甚至可以说，我们还处在第三次数学危机中3。

本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学