科技工作者之家
科技工作者之家APP是专注科技人才,知识分享与人才交流的服务平台。
科技工作者之家 2020-11-17
雷米兹算法,或称雷米兹交换算法,由叶夫根尼·列维奇·雷米兹于1934年所发表。 雷米兹算法为一寻找函式简易近似之迭代算法,特别是定义于切比雪夫空间的函式效果最佳。
一个在切比雪夫空间的典型例子是 n 次项切比雪夫多项式的子空间,属于实数连续函式之向量空间,定义于 C[a, b] 区间。
给定一子空间,其最佳近似多项式的定义为:可将此近似多项式与原始函式之最大绝对差异最小化者。 在这个情况下,可由equioscillation theorem使其解更精确.
程序雷米兹算法由一函式f开始,欲近似一集合X,且在近似的区间上工有 个取样点
个取样点 , 通常Chebyshev nodes可映射至该区间,步骤如下:
, 通常Chebyshev nodes可映射至该区间,步骤如下:
解线性系统之等式
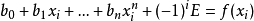 (其中
(其中 ),
),
对于未知的 及E。
及E。
使用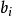 作为多项式
作为多项式 的系数。
的系数。
找出集合M,为 之区域极大错误点。
之区域极大错误点。
若在 之中的所有
之中的所有 都是相同大小,仅正负号不同的话,则
都是相同大小,仅正负号不同的话,则 为极小化极大近似之多项式。若否,则M取代X并重复上述步骤。
为极小化极大近似之多项式。若否,则M取代X并重复上述步骤。
此结果称为最佳近似多项式、切比雪夫近似、或最小化最大近似。
初始化选择由于切比雪夫节点在多项式插值理论中所扮演的脚色,故通常选择其为初始近似的方法。由拉格朗日插值法Ln(f) 初始化一函式f之最佳化问题,可以证明此初始近似之边界限制为:
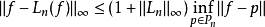 其中节点 (t1, ...,tn+1) 之拉格朗日插值法算子的常数为
其中节点 (t1, ...,tn+1) 之拉格朗日插值法算子的常数为
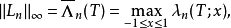 T为切比雪夫多项式的零点,而
T为切比雪夫多项式的零点,而
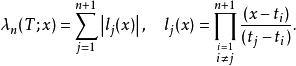 对提供次最佳之切比雪夫节点来说,其渐进线为
对提供次最佳之切比雪夫节点来说,其渐进线为
 (γ为欧拉-马歇罗尼常数),
(γ为欧拉-马歇罗尼常数),
 而上界为
而上界为
 Lev Brutman 计算出对
Lev Brutman 计算出对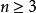 的边界,而
的边界,而 为切比雪夫多项式之零点
为切比雪夫多项式之零点
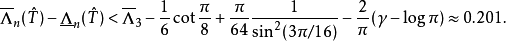 Rüdiger Günttner由对
Rüdiger Günttner由对 之较粗略的估算计算出
之较粗略的估算计算出

细节讨论在此将提供先前简述步骤的详细内容1,在这个章节令指数i从 0 跑到n+1.
**步骤 1:**给定 , 求n+2 条等式之线性系统之解
 (其中
(其中 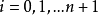 ),
),
对于未知的 和E.
和E.
可以很清楚地观察到,在这个式子里 若要成立,只有在节点
若要成立,只有在节点 为排序的情况下才能达到,无论是严格递增或递减。这样一来这个线性系统便有唯一解。(广为人知的,并非每个线性系统都可以求解)。 此外,求解之复杂度最少为
为排序的情况下才能达到,无论是严格递增或递减。这样一来这个线性系统便有唯一解。(广为人知的,并非每个线性系统都可以求解)。 此外,求解之复杂度最少为 ,而一个从函式库求解的标准计算器需要
,而一个从函式库求解的标准计算器需要 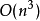 的复杂度,在此有一简单证明:
的复杂度,在此有一简单证明:
计算前n+1个节点之{\displaystyle f(x)}标准n阶插值  , 以及对于{\displaystyle (-1)^{i}}之标准n阶插值
, 以及对于{\displaystyle (-1)^{i}}之标准n阶插值
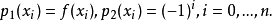 至此,需要
至此,需要  次数值运算。
次数值运算。
在 与
与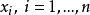 之间,多项式
之间,多项式 有其i-阶 零点zero between
有其i-阶 零点zero between 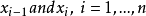 ,因此在
,因此在  与
与  之间无任何零点,意即
之间无任何零点,意即 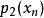 与
与  正负号
正负号 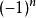 相同。
相同。
线性组合 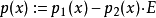 亦为一n次多项式
亦为一n次多项式
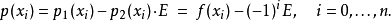 选择任何E,对
选择任何E,对 ,下列式子与上述等式相同:
,下列式子与上述等式相同:
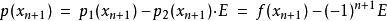 解E得:
解E得:
 如前述所提及,上式分母之两项有相同正负号,因此
如前述所提及,上式分母之两项有相同正负号,因此
 是完整定义的。
是完整定义的。
给定n+2 阶节点,其误差为正负轮流:
 de La Vallée Poussin理论说明在这种形况下,没有误差少于E之n次多项式存在。
de La Vallée Poussin理论说明在这种形况下,没有误差少于E之n次多项式存在。
步骤 2把多项式表示由 转为
转为  .
.
步骤 3依照以下所述改善输入节点 的误差{\displaystyle \pm E}。
的误差{\displaystyle \pm E}。
在每个 P-领域,现在的节点 将被区域最大
将被区域最大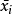 取代,同样在每个 N-领域,
取代,同样在每个 N-领域,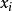 将被区域最小取代, 在这部分并不要求高精确律。2
将被区域最小取代, 在这部分并不要求高精确律。2
令 , 其大小
, 其大小 皆大于或等于E。de La Vallée Poussin理论及其证明也可以应用至
皆大于或等于E。de La Vallée Poussin理论及其证明也可以应用至 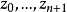 , 而使此n次多项式有最小可能误差的新下界为
, 而使此n次多项式有最小可能误差的新下界为 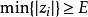 。
。
**步骤 4:**分别以 与
与 为新的上下界,此迭代算法的终止条件为: 重复上述步骤直到
为新的上下界,此迭代算法的终止条件为: 重复上述步骤直到 足够小且不再递减。
足够小且不再递减。
变异有时候在最大绝对差异点的附近,会有复数个点同时被取代。
有时候相对误差会被用来衡量函式与其近似的差异,特别是在电脑上用浮点数做运算的函式。
本词条内容贡献者为:
胡建平 - 副教授 - 西北工业大学