全等球面三角形

全等球面三角形(congruent spherical triangles)是指两个球面三角形的一种等价关系，即在同球面或等球面上，一个球面三角形的三边、三角分别与另一个球面三角形的三边、三角对应相等的两个球面三角形1。

基本概念全等球面三角形：（1）在同一球或等球面上，若两球面三角形的边及角分别对应相等，且排列顺序一致时，则称这两个球面三角形为全等。

（2）全等球面三角形指在同球面或等球面上，一个球面三角形的三边、三角分别与另一个球面三角形的三边、三角对应相等的两个球面三角形。全等球面三角形可分为两类：1.定向相同的(称为本质相等的球面三角形或绝对相等的球面三角形)；2.定向相反的(称为镜像相等的球面三角形)1。

以上两个定义第（1）个定义实际上是第（2）个定义中的绝对相等的球面三角形，有的书籍上是第（1）种定义，有的书籍上是第（2）种定义。

一般所说全等球面三角形指的是第（1）种定义中所说的情形。

球面三角形全等的条件在同球面或等球面上，具备下列条件之一的两个球面三角形全等：

1) 两角及其夹边对应相等。

2) 两边及其夹角对应相等。

3) 两角及其中一角的对边对应相等，且其他两角的对边都小于一象限，或都大于一象限。

4) 两边及其中一边的对角对应相等，且其他两边的对角均为锐角，或均为钝角。

5) 三边对应相等。

6) 三角对应相等1。

详细介绍对称球面三角形是全等球面三角形如图1，设在同一个球面上两个三角形ABC和A'B'C'关于大圆l对称，那么大圆弧AA'被大圆l垂直平分。

不难看出：A和A'关于l所在平面成镜面反射。同样地，B和B'，C和C'都关于I所在平面成镜面反射2。

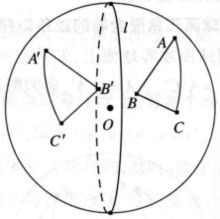
如果以球心O为端点，连接OA，OB，OC作三条射线，就可以得到一个类似于三棱锥O-ABC形状的“空间角”，它由三棱锥的三个侧面围成，我们把它称为三面角，记为三面角O- ABC，同样方法还可以得到三面角O-A'B'C'。 因此，三面角O-ABC与三面角O-A'B'C'也关于l所在平面成镜面反射。所以，它们的三个面上的平面角分别相等。

即：∠AOB=∠A'OB'，

∠COA=∠C'OA'，

∠BOC=∠B'OC'，

由此得到a=a'，b=b'，c=c'。

这两个三面角的三个二面角也分别相等，由此得到：

∠A=∠A'，∠B=∠B'，∠C=∠C'，

因此，球面三角形ABC全等于球面三角形A'B'C'，记为：

△ABC≌A'B'C'。

于是：

同一球面上，对称的两个球面三角形也是全等的三角形2。

全等球面三角形的边角边判定定理在平面上，如果两个三角形中，有两组对边及其夹角对应相等，那么这两个三角形全等。这是平面几何关于两个三角形全等的判定定理。球面几何是否也有类似的结论?答案是肯定的。

在同球面或等球面上，如果两个球面三角形的两组对边及其夹角对应相等,那么这两个球面三角形全等。

这个性质称为两个球面三角形全等的边角边判定定理。

如图2，设在同球面或等球面上，如果在两个球面三角形ABC和A'B'C'中，AB=A'B'，AC=A'C'，∠A=∠A’，要判断这两个球面三角形是否全等，可以用重合法。

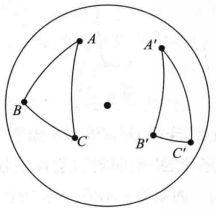
我们在平面几何里也常用重合法进行证明，就是通过移动把一个图形转移到与另一个图形重合的位置，从而得到所需的结论。平面几何运用重合法的依据，是平面的对称性。因为球面和平面的对称性类似，在球面几何中，也可以用重合法进行证明。

利用球面的对称性，根据AB =A'B'，可以移动球面三角形A'B'C'，使A'B'落在AB的位置，弧的端点A'与A重合，B'与B重合。

这时,大圆AB把球面分成两半，这就看C'落在哪个半球上，再分成两种情况分别讨论。

(1)若C'落在包含C的半球面内，由于∠A=∠A'，可知大圆弧A'C'落在AC上，又AC=A'C'，所以C'落在C上。因而球面三角形A'B'C'的新位置与球面三角形ABC重合,所以这两个球面三角形全等。

(2)若C'落在另外的半球面上,那么利用类似(1)的理由，可知球面三角形A'B'C'的新位置与球面三角形ABC对称，所以这两个球面三角形全等2。

全等球面三角形的边边边判定定理平面上三边对应相等的两个三角形全等，球面三角形是否也有这样的性质?

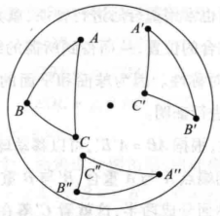
如图3，设在同球面或等球面上，有两个球面三角形ABC和A'B'C'，它们的三对对应边相等，即a=a',b=b',c=c'。

(1)如果三角形ABC与A'B'C'方向相同，这时,由于它们在同球面或等球面上，所以可以通过移动使A与A'重合，C与C'重合，自然B与B'重合。由于a=a',b=b'，所以C与C'一定重合。因此，这两个球面三角形可以完全重合。

(2)如果△ABC与A'B'C'方向不相同，如图3，先作△ABC的球面对称三角形A"B"C"，由球面对称三角形的性质,有：

△ABC≌△A"B"C"。

这时，△A"B”C"与△A'B'C'方向相同且对应边相等，所以△A"B"C"≌△A'B'C'即△ABC≌△A'B'C'。

也就是说：

在同球面或等球面上，如果两个球面三角形的三对对应边相等，那么这两个球面三角形全等。

这个性质称为两个球面三角形全等的边边边判定定理2。

全等球面三角形的角边角判定定理此外，我们还有如下性质:

在同球面或等球面上，如果两个球面三角形的两对对应角和它们的夹边对应相等，那么这两个球面三角形全等。

这个性质称为两个球面三角形全等的角边角判定定理。

此定理的证明也可以用重合法证明，读者可以试一试。

通过上面的讨论，我们会发现，平面上两个三角形全等的概念及判定全等的边角边定理，边边边定理，角边角定理都可以推衍到球面上，但是要注意，这些概念和性质只能在同--球面或半径相等的球面上讨论，只有满足这一条件，上述判定定理才能成立2。

全等球面三角形的角角角判定定理初中老师在学习平面几何时，常常要提醒“如果两个三角形的三组对应角相等，只能判断它们相似，但不一定全等”；而球面上，我们却可以大大方方地把“不”字去掉，因为我们可以用极三角形性质，严格证明如下的结论：

在同球面或等球面上，如果两个球面三角形的三组对应角对应相等，那么这两个球面三角形全等。

这个性质称为两个球面三角形全等的角角角判定定理。

从以上讨论可以看到，球面三角形全等和平面三角形全等虽然有很多性质都相同，比如角边角、边角边、边边边判定定理。但是球面三角形全等却增加了一个角角角判定定理，这个定理在平面几何中只能作为两个三角形相似的判定定理。球面上的几何和平面上的几何存在很多相似之处，但也存在着巨大差别2。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学