科技工作者之家
科技工作者之家APP是专注科技人才,知识分享与人才交流的服务平台。
科技工作者之家 2020-11-17
反对称变换(anti-symmetric transformation)是一种线性变换,设V是欧氏空间,σ是V的线性变换,若对任意α,β∈V,有(σ(α),β)=-(α,σ(β)),则称σ为V的反对称变换。反对称变换对于有限维欧氏空间V的任意标准正交基的矩阵是实反对称矩阵,即为满足条件A′=-A的实矩阵;反之,若线性变换关于V的标准正交基的矩阵是反对称的,则σ是反对称变换,反对称变换的特征值或是零,或是纯虚数1。
基本介绍针对对称变换,我们把欧氏空间中对任意 ,满足
,满足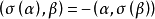 的线性变换
的线性变换 叫做反对称变换。
叫做反对称变换。
【例1】在欧氏空间R2中,规定线性变换σ为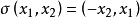 ,证明:σ是反对称变换。
,证明:σ是反对称变换。
证明: 因为对任意 ,有:
,有:
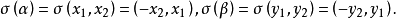
于是,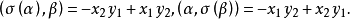
所以,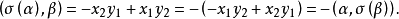
故σ是反对称变换。
反对称变换的性质根据反对称变换的定义,可以证得反对称变换的以下一些性质:
定理1 欧氏空间V的线性变换σ是反对称变换的充分必要条件是σ关于V的标准正交基的矩阵是反对称矩阵。
证明 设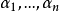 是V的组标准正交基,且
是V的组标准正交基,且
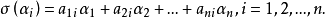 于是,
于是, .
.
所以,σ是反对称变换的充分必要条件是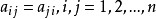 ,即σ关于V的标准正交基f内矩阵是反对称矩阵。
,即σ关于V的标准正交基f内矩阵是反对称矩阵。
性质1 设σ是欧氏空间V的反对称变换,如果V1是σ的不变子空间,则也是σ的不变子空间。
证明 对任意的向量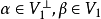 ,有
,有 而V1是σ的不变子空间,所以
而V1是σ的不变子空间,所以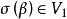 ,故
,故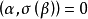 ,于是得
,于是得 .因此
.因此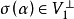 ,即
,即 是σ的不变子空间。
是σ的不变子空间。
性质2 设σ是欧氏空间V的反对称变换,则σ的特征根是零或纯虚数。
证明 设σ是欧氏空间V的反对称变换,A是σ关于V的某个标准正交基的
矩阵,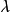 是A的任一特征根,α是属于特征根
是A的任一特征根,α是属于特征根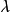 的特征向量,则有:
的特征向量,则有:
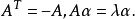
一方面, 另一方面,有:
另一方面,有:

所以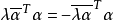 ,但
,但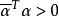 ,从而
,从而 ,故反对称实矩阵的特征根是零或纯虚数,即σ的特征根是零或纯虚数。
,故反对称实矩阵的特征根是零或纯虚数,即σ的特征根是零或纯虚数。
和对称变换一样,因反对称变换与反对称矩阵一一对应,所以反对称变换所具有的性质,反对称矩阵都具有,这里从略2。
本词条内容贡献者为:
胡建平 - 副教授 - 西北工业大学