扩展欧几里得算法

扩展欧几里得算法是欧几里得算法（又叫辗转相除法）的扩展。除了计算a、b两个整数的最大公约数，此算法还能找到整数x、y（其中一个很可能是负数）。通常谈到最大公因子时, 我们都会提到一个非常基本的事实: 给予二整数 a 与 b, 必存在有整数 x 与 y 使得ax + by = gcd(a,b)。有两个数a,b，对它们进行辗转相除法，可得它们的最大公约数——这是众所周知的。然后，收集辗转相除法中产生的式子，倒回去，可以得到ax+by=gcd(a,b)的整数解。

简介扩展欧几里得算法（英语：Extended Euclidean algorithm）是欧几里得算法（又叫辗转相除法）的扩展。已知整数a、b，扩展欧几里得算法可以在求得a、b的最大公约数的同时，能找到整数x、y（其中一个很可能是负数），使它们满足贝祖等式

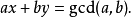如果a是负数，可以把问题转化成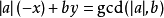，然后令x'=(-x)。

通常谈到最大公约数时，我们都会提到一个非常基本的事实：给予二个整数a、b，必存在整数x、y使得ax + by = gcd(a,b)。

有两个数a,b，对它们进行辗转相除法，可得它们的最大公约数——这是众所周知的。然后，收集辗转相除法中产生的式子，倒回去，可以得到ax+by=gcd(a,b)的整数解。

扩展欧几里得算法可以用来计算模反元素(也叫模逆元)，而模反元素在RSA加密算法中有举足轻重的地位。

例子用类似辗转相除法，求二元一次不定方程47x+30y=1的整数解。1

过程可以用矩阵表示（其中q表示商，r表示余数）。

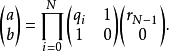
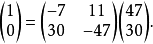
或者用初等变换

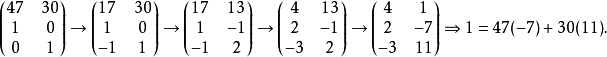
实现以下是扩展欧几里德算法的Python实现：

def ext_euclid(a, b): if b == 0: return 1, 0, a else: x, y, q = ext_euclid(b, a % b) # q = gcd(a, b) = gcd(b, a%b) x, y = y, (x - (a // b) * y) return x, y, q扩展欧几里得算法C语言实现：

int gcdEx(int a, int b, int *x, int *y) { if(b==0) { *x = 1,*y = 0; return a; } else { int r = gcdEx(b, a%b, x, y); /* r = GCD(a, b) = GCD(b, a%b) */ int t = *x; *x = *y; *y = t - a/b * *y; return r; } }本词条内容贡献者为:

李岳阳 - 副教授 - 江南大学