圆簇

圆簇(family of circles)亦称共幂圆系，是平面几何术语。指具有某种共性的圆的集合，即有公共根心的圆的全体。公共的根心称为圆簇的中心，该中心对圆簇中每一个圆的幂都是相等的，这个值称为圆簇的幂。若圆簇的幂是正的，则这个圆簇称为双曲型圆簇；若圆族的幂是负的，则这个圆簇称为椭圆型圆簇；若圆簇的幂为零，则这个圆簇称为抛物型圆簇1。

基本介绍有公共等幂心的圆的集合叫做圆簇。这公共等幂心叫做该能的中心；等幂心对于簇内每个圆的幂叫做圆簇的幂。如果圆簇的幂是正的，则该簇叫做双曲线型圆簇；如果是负的，则该簇叫做椭圆型圆簇；如果幂等于零，则该簇叫做抛物线型圆族。

双曲线型圆簇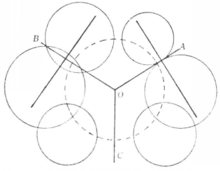

图1表示双曲线型圆簇，圆簇的中心到簇内所有圆的切线都相等，即有一个以图簇中心为圆心，幂的平方根为半径的圆，圆与簇内所有圆都垂直相交，这个圆叫做双曲线型圆簇的基圆(如图1中的⊙O)，在双曲线型圆簇中包含着三种类型的圆束，即抛物线型圆束的等幂轴用OB表示，此圆束的连心线不与基圆相交；双曲线型圆束的等幂轴用OC表示，此圆束的连心线与基圆相交。

椭圆型圆簇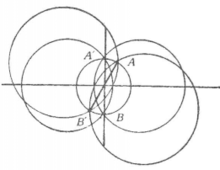

图2表示椭圆型圆簇，如果圆簇中心O对于所有圆的幂都是负的，则以圆簇的中心为圆心，以幂的绝对值的平方根为半径作⊙O，于是椭圆型园簇的一切圆都交⊙O的直径的两端，例如AB。因此⊙O的每一直径AB都是某种椭圆型圆束的等幂轴，而直径的两端是该束中所有圆的交点。由此可知，椭圆型圆簇只包括椭圆型圆束，而⊙O是圆簇中最小的圆，也是簇内各圆束所共有的圆。

抛物线型圆簇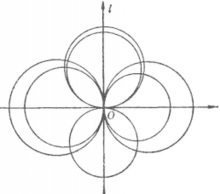

图3表示抛物线型圆簇，在这种情况下，簇内所有圆都应该通过簇的中心O，因为点O对于簇内所有圆的幂都等于零，所以抛物线型圈簇内有抛物线及椭圆型的圆束，而没有双曲线型圆束。

相关介绍(1)设过一定点作一动直线与一定圆相交,则自定点至两交点的两个有向线段的积是一个常数。这是初等几何中大家已熟知的定理，那个常数的值，我们称它做定点对于定圆的幂；它的平方根叫做幂根，因为幂的值可为正、负或零，所以幂根的值随着为实、虚或零，当定点在定圆的外部时，它的幂根可以用定点至定圆的切线长来表示；在圆内时，可以用过定点的极小弦的半长乘以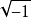 来表示；若在圆上,幂根的值便为零了2。

上面的定义，乃系对于通常的实圆而说的，为着避免牵扯，关于虚圆的说法，我们不必去谈(虽然后面也有提及虚圆的，不过只是路一提及，不去探究)，以后有些地方，万一涉及虚圆的,那就用另一方式去代替说明，除虚圆外，圆还有他种变形，譬如，半径无穷增大而变为直线，半径无穷减小而变为点，为着使我们的定义含义丰富，对于这些广义的圆一直线 、无穷远线及零圆(点)一来说，共意义仍须加以修饰一下，也可以说是规定一下；这样对于我们以后的叙述才不会受到它们的掣肘，并且还可以使意义普遍化。

①定圆为直线，我们先这样设想：令P为定点，自P作一直线k通过⊙O的中心而交⊙O于A，B，则P对于⊙O的幂为

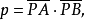
而后固定点A ，使⊙O的半径渐渐增大，即点O在k上渐趋于无穷远，那么⊙O的极限状态就要变成直线l的形状，而B在k上也趋至无穷远的位置，这时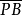 的值便变成无穷大，这就是说，直线外的任何点对于这直线的幂是无穷大。若p在l上，即P和A相合，那么 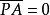，这时我们自然要把p看做不定值，这样一来，当直线和圆混杂在一起而组成某某类的时候，我们就可以把直线上的点对于直线的幂看成与对于圆的幂有某种的关系(例如相等)了，这种看法在下款我们就要用到，希望读者记着。

②定圆为无穷远线，无论定点是通常的点或无穷远点，一律规定它对于无穷远线的幂是无穷大。

③定圆为零圆(点)，这时定点对于零圆的幂，就用它们间的距离的平方来表示。

我们有了这些概念，直线、无穷远线零圆和通常的圆在某种条件下的关联便可以建立起来了。

(2)平面上两个不同的圆，假设一个动点对于它们的幂是相等的，那么这个动点的轨迹是一条直线，这条直线就叫做那两个圆的等幂轴.这在初等几何中，大家一定很熟悉的了，这种特性，无论两个圆是通常的圆抑其中有一或全是零圆，都可以适合，但若其中有一或全是直线(或有一是无穷远线)的话，那我们仍须规定一下:

①一圆(或零圆)和一直线(或无穷远线)的等幂轴就是那直线(或无穷远线)的本身。

②两直线(或有一是无穷远线)的等幂轴是通过它们的交点的任一直线(不定)。

有了这个规定之后，那我们以后凡说圆的，都可以同时包括通常的圆、零圆、直线和无穷远线，不再另加说明了；但有时为了使得更加明了，也不妨特别指明。

平面上许多圆，倘若它们之间两两的等幂铀都相合为一，那么这许多圆所组成这样的一群，我们就称它做共轴圆系，这个共轴圆系的等幂轴，亦应当包括在里面而为系中的一员，由此我们可以知道，平面上两个不同的圆，必定完全确定一个唯一的共轴圆系2。

平面上有三个不同的圆，假定它们不属于同--的共轴圆系，那么它们便两两确定三个不同的共轴圆系，这三个共轴圆系的等幂轴，我们很容易知道一般都是同交于一点，只三个圆全为直线时是例外，这个点我们就称它做那三个圆(因而也是那三个共轴圆系的全体)的等幂心；至于三条直线的等幂心我们当然认为是个不定点，现在平面上有许多圆，它们不属于同一的共轴圆系，倘若它们之间三三的等幂心都相合为一。那么这许多圆所组成这样的一群，我们就称它做共幂圆系、通常地说，这个共幂圆系的等幂心对于每圆的幂必定彼此相等‘’所以我们以等幂心为圆心，等幂心对于各圆的幂根为半径，必定作得一个唯一的圆，这个圆我们叫它做这个共幂圆系的等幂圆，再进一步说，因为幂根的值可以为实、为虚、为无穷大或为零，所以等幂圆就有实圆、虚圆、直线(或无穷远线)或零圆等的区别。显然，当等幂圆是实圆或直线的时候，它一定同时正交于系中的每一圆，即是它恰为系中各圆的唯一公共正交圆。

为着易于掌握共幂圆系的性质，我们要把它分成下面的几类，如此逐类去研究，那就比较容易明了了，分类的着眼点，要从等幂圆来人手:

第一类，等幂圆为实圆，这时等幂心在系中各通常圆的外部，此类包括通常圆(圆心在等幂圆外)、零圆(等幂圆上的点)及通过等幂心的直线，也就是凡正交于一定实圆的圆，便组成第一类的共幂圆系。

第二类，等幂圆为虚圆，这时等幂心在系中各通常圆的内部，此类包括通常圆及通过等幂心的直线，设过等幂心作各圆的极小弦，则易知所得各弦都等长。而且有一个共同中点(即等幂心) ，故以各弦为直径可作得一个唯一的圆。因此，这类共幂圆系我们也可以说是径交于一定实圆的那些圆。

第三类，等幂圆为直线，这时等幂心为此线的垂线上的无穷远点，此类包括通常的圆(圆心在等幂圆上)零圆(等幂圆上的点)、垂直于等幂圆的直线及无穷远线，亦即凡正交于一定直线的圆，便组成第三类的共幂圆系。

第四类，等幂圆为零圆，这时等幂心就是等幂圆，它必定同时在系中各圆的上面，故此类共幂圆系亦即共点的一群圆，包括通常的圆、一零圆(即等幂心)及通过等幂心的直线。

第五类，等幂圆为无穷远线，这时凡是直线及该无穷远线的本身都属于此类共幂圆系，这类对于上面的几类来说，其中有一个特异的地方：把无穷远线看做圆。圆心就不是一个固定的点。所以这类共幂圆系的等幂心应当是个不定点，因而把前几类等幂心的唯一性的特征消失掉了、

(3)共幂圆系经反演变换后。仍为共幂圆系。这在第一，第三。第四。第五四类来看。是很容易知道的。因为正交圆和共点圆这种属性乃是反演不变的性质的缘故但对于第二类共幂圆 系是否也是如此呢?为要证实它一样具有这种特性。我们可以这样设计:假定取一点O为反演中心，设P为等幂心。P对于系中各圆的幂为p，而在OP上取一点Q，仅适合

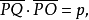那么通过O，Q的一群圆便组成一一个共轴圆系，这系中的每一圆显然都属于原来的共幂圆系，而且在后者中任取两圆，则在前者中必有一圆与之共轴，经过反演之后，上述的那个共轴圆系的各圆便都变成共点的直线，而原共幂圆系各圆的反演圆中每两圆的等幂轴也就不出于这些直线，于是我们的目的达到了，现在把各类共幂圆系相互间的反演变换情形列下:

①第-类经反演后，类别通常不变；但若以等幂圆上的点为反演中心，则反演为第三类。

②第二类经反演后，类别不变。

③第三类经反演后，通常变为第--类；但若以等幂圆上的点为反演中心，则类别不变。

④第四类经反演后，类别通常不变；但若以等幂心为反演中心，则反演为第五类。

⑤第五类经反演后，通常变为第四类；但若反演基圆为直线(此时等于施行线反射)，则类别不变2。

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学