科技工作者之家
科技工作者之家APP是专注科技人才,知识分享与人才交流的服务平台。
科技工作者之家 2020-11-17
反复残差法将模型线性化的一种迭代算法,由Subba Rao在处理双线性模型时提出。 Subba Rao提出了反复残差法估算模型参数,该法是在假定模型阶数、模型参数初值和计算精度条件下,计算模型残差平方和,在最小二乘意义下使其极小化,估计新的参数值,再求残差平方和。如此反复迭代,直到满足要求的精度,这时的参数值即为所求。模型定阶采用AIC。反复残差法有计算量大,操作不便的缺点1。
基本介绍双线性差分方程 对零均值时序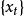 拟合的双线性模型为**:**
拟合的双线性模型为**:**
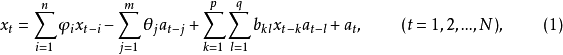 记该模型为BM(n,m,p,q),其中,残差
记该模型为BM(n,m,p,q),其中,残差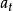 为方差是
为方差是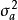 的白噪声,当
的白噪声,当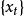 是非零均值时,上式中还应有一常数项
是非零均值时,上式中还应有一常数项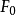 。
。
式(1)较ARMA (n, m)模型多一个双线性项,即当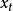 固定时,变成关于
固定时,变成关于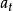 的线性模型,当
的线性模型,当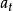 固定时,变成了关于
固定时,变成了关于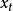 的线性模型,因而称之为双线性模型。可以把双线性模型视为ARMA模型的推广。但是,由于它是非线性模型,模型的定阶准则,稳定性与可逆性等比ARMA模型的复杂得多,计算也困难得多。对某些较简单的双线性模型,建模时可沿用线性系统的定阶准则,如F检验,AIC准则等。
的线性模型,因而称之为双线性模型。可以把双线性模型视为ARMA模型的推广。但是,由于它是非线性模型,模型的定阶准则,稳定性与可逆性等比ARMA模型的复杂得多,计算也困难得多。对某些较简单的双线性模型,建模时可沿用线性系统的定阶准则,如F检验,AIC准则等。
在阶数已确定的情况下,对于双线性模型的参数估计问题,原则上与线性模型的处理方法相同,现叙述如下,在式(1)中,当N足够大时,有似然函数,
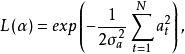 式中,
式中,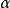 为参数的集合,
为参数的集合,
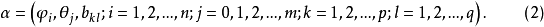 于是,
于是,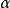 的极大似然估计为使残差平方和
的极大似然估计为使残差平方和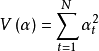 达最小,即
达最小,即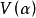 对
对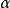 中每个元素取极小化而得到,因此,关于ARMA模型的建模方法如Levinson算法一般均适用于双线性建模。Subba Rao提出的“反复残差法”对较为简单的双线性建模颇为方便有效,其思路可由图1说明。图中Z是由{xt}中的元素构成的列向量,A是
中每个元素取极小化而得到,因此,关于ARMA模型的建模方法如Levinson算法一般均适用于双线性建模。Subba Rao提出的“反复残差法”对较为简单的双线性建模颇为方便有效,其思路可由图1说明。图中Z是由{xt}中的元素构成的列向量,A是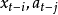 与
与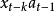 所构成的己知的常数矩阵,
所构成的己知的常数矩阵,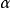 是式(2)所示的模型参数构成的列向量,反复残差法是在模型阶数已知的条件下建模2。
是式(2)所示的模型参数构成的列向量,反复残差法是在模型阶数已知的条件下建模2。
|| || 反复残差法建模
实例分析下面是一个简单的双线性模型的建模过程2。
设要建立的双线性模型为:
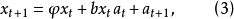 即
即
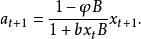 式中,B为后移算子,当b较小时,近似地有
式中,B为后移算子,当b较小时,近似地有
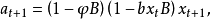 即
即
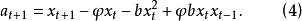 忽略
忽略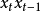 项,则有
项,则有
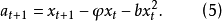 于是可应用最小二乘法估计参数φ、 b,如不忽略
于是可应用最小二乘法估计参数φ、 b,如不忽略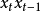 项,则可应用非线性最小二乘法估计参数。
项,则可应用非线性最小二乘法估计参数。
设参数的初始估值为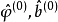 , 则由式(5)可得其残差的初值
, 则由式(5)可得其残差的初值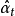 ,根据式(3) 求残差平方和
,根据式(3) 求残差平方和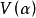 。
。
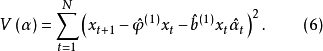 在最小二乘意义下使其极小化,估计新的参数值
在最小二乘意义下使其极小化,估计新的参数值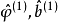 ,再将新参数代入式( 3)求残差,
,再将新参数代入式( 3)求残差,
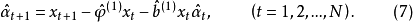 求出新的残差后,再代入式(6),估计新的参数
求出新的残差后,再代入式(6),估计新的参数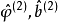 ,如此反复迭代,直到满足精度为止2。
,如此反复迭代,直到满足精度为止2。
仿真建模实例
设双线性差分方程为:
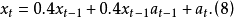 图1所示为该双线性系统的时间序列,系统的输入
图1所示为该双线性系统的时间序列,系统的输入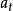 是方差
是方差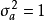 的零均值的白噪声,图2所示为双线性时序的概率密度分布图,其中虚线为实际分布,实线为正态分布,可见该序列已不是正态分布;图中示出了序列的均值、方差、偏态值与峰态值,从中也可看出其非线性的特性。表1列出了双线性建模的结果。其中,F0为模型中含有的常数项,以便于拟合均值不为零的时序,将表中结果与式(8) 比较可知,两者符合情况较好,表明反复残差法建模是有效的2。
的零均值的白噪声,图2所示为双线性时序的概率密度分布图,其中虚线为实际分布,实线为正态分布,可见该序列已不是正态分布;图中示出了序列的均值、方差、偏态值与峰态值,从中也可看出其非线性的特性。表1列出了双线性建模的结果。其中,F0为模型中含有的常数项,以便于拟合均值不为零的时序,将表中结果与式(8) 比较可知,两者符合情况较好,表明反复残差法建模是有效的2。
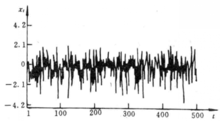
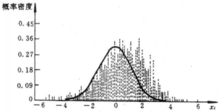
均值:-0.317177 偏态:-0.347777 方差:1.543746 峰态:1. 005134
|| || 表1 双线性建模结果
本词条内容贡献者为:
杜强 - 高级工程师 - 中国科学院工程热物理研究所