科罗夫金定理

科罗夫金定理是正线性算子序列逼近的基本定理。20世纪50年代，由科罗夫金建立。

简介科罗夫金定理是正线性算子序列逼近的基本定理。

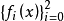20世纪50年代，科罗夫金建立了如下的定理：设 是C[a,b]到C[a,b]的正线性算子序列， 是[a,b]上的一个切比雪夫组。如果n→∞时，Ln(f,x)在[a,b]上一致收敛于fi(x)(i=0,1,2)，则对于任何f∈C[a,b]，当n→∞时，Ln(f,x)都在[a,b]上一致收敛于f(x)，常称这个定理为科罗夫金定理。又称这三个函数f0(x),f1(x)和f2(x)为试验函数。

适用条件对于函数空间C[a,b]，常取fi(x)=xi(i=0,1,2)，而对于函数空间C2π，常取f0(x)=1，f1(x)=cos x，f2(x)=sin x。

在科罗夫金定理中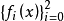， 构成一个切比雪夫组这个条件是必要的。因为科罗夫金还证明了如下的结论：设fi∈C[a,b](i=0,1,2)，如果对于每个C[a,b]到C[a,b]的正线性算子序列 ，从n→∞时Ln(fi,x)(i=0,1,2)在[a,b]上一致收敛就能推出，对任何f∈C[a,b]都有n→∞时Ln(f,x)在[a,b]上一致收于f(x)，则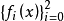 一定是切比雪夫组。

正线性算子逼近正线性算子逼近是一类常用的逼近。

设f∈C[a,b]，如果对一切x∈[a,b]都有f(x)≥0则记f≥0。设L是C[a,b]到C[c,d]的线性算子，[c,d]⊂[a,b]，如果对f≥0有L(f)≥0，则称L为正线性算子。

此时用L(f,x)在[c,d]上逼近f(x)称为正线性算子逼近。1

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学