科技工作者之家
科技工作者之家APP是专注科技人才,知识分享与人才交流的服务平台。
科技工作者之家 2020-11-17
库利-图基快速傅里叶变换算法(Cooley-Tukey算法)1是最常见的快速傅里叶变换算法。这一方法以分治法为策略递归地将长度为N = N1N2的DFT分解为长度分别为N1和N2的两个较短序列的DFT,以及与旋转因子的复数乘法。
简介这种方法以及FFT的基本思路在1965年J. W. Cooley和J. W. Tukey合作发表An algorithm for the machine calculation of complex Fourier series之后开始为人所知。但后来发现,实际上这两位作者只是重新发明了高斯在1805年就已经提出的算法(此算法在历史上数次以各种形式被再次提出)。
库利-图基快速傅里叶变换算法是将序列长为N的DFT分区为两个长为N/2的子序列的DFT,因此这一应用只适用于序列长度为2的幂的DFT计算,即基2-FFT。实际上,如同高斯和库利与图基都指出的那样,库利-图基算法也可以用于序列长度N为任意因数分解形式的DFT,即混合基FFT,而且还可以应用于其他诸如分裂基FFT等变种。尽管库利-图基算法的基本思路是采用递归的方法进行计算,大多数传统的算法实现都将显示的递归算法改写为非递归的形式。另外,因为库利-图基算法是将DFT分解为较小长度的多个DFT,因此它可以同任一种其他的DFT算法联合使用。
复杂度离散傅立叶变换的复杂度为 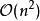 (可引用大O符号)。快速傅立叶变换的复杂度为
(可引用大O符号)。快速傅立叶变换的复杂度为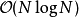 ,分析可见下方架构图部分,级数为
,分析可见下方架构图部分,级数为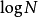 而每一级的复杂度为
而每一级的复杂度为 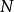 ,故复杂度为
,故复杂度为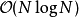 。
。
时域-频域抽取法在FFT算法中,针对输入做不同方式的分组会造成输出顺序上的不同。如果我们使用时域抽取(Decimation-in-time),那么输入的顺序将会是比特反转排列(bit-reversed order),输出将会依序排列。但若我们采取的是频域抽取(Decimation-in-frequency),那么输出与输出顺序的情况将会完全相反,变为依序排列的输入与比特反转排列的输出。

时域抽取法我们可以将DFT公式中的项目在时域上重新分组,这样就叫做时域抽取(Decimation-in-time),在这里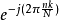 将会被代换为旋转因子(twiddle factor)
将会被代换为旋转因子(twiddle factor) 。
。

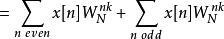

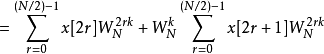

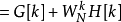
在这边我们要注意的是,我们所替换的G[k]与H[k]具有周期性:

上述的推导可以划成下面的图:
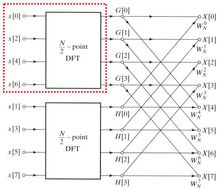
划红框处所示的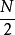 点DFT架构如下图所示:
点DFT架构如下图所示:
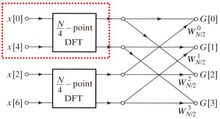
划红框处所示的 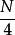 点DFT架构如下图所示:
点DFT架构如下图所示:
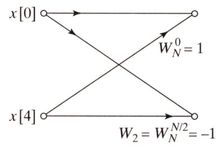
下图是一个8点DIT FFT的完整架构图。

频域抽取法我们可以将DFT公式中的项目在频域上重新分组,这样就叫做频域抽取(Decimation-in-frequency)。
首先先观察在频域上偶数项的部分:


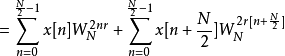
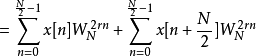
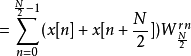
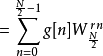
再观察在频域上奇数项的部分:

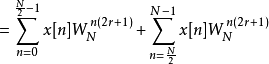

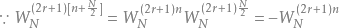

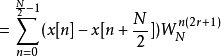


上述的推导可以画成下面的图:

更进一步的拆解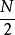 -point DFT的架构
-point DFT的架构

下图为8点FFT下 -point DFT的架构
-point DFT的架构

总结上述架构,完整的8点DIF FFT架构图为
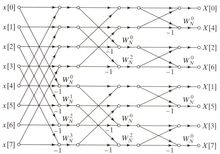
单一基底利用库利-图基算法进行离散傅立叶拆解时,能够依需求而以2, 4, 8…等2的幂次方为单位进行拆解,不同的拆解方法会产生不同层数快速傅里叶变换的架构,基底越大则层数越少,复数乘法器也越少,但是每级的蝴蝶形架构则会越复杂,因此常见的架构为2基底、4基底与8基底这三种设计。
2基底2基底-快速傅立叶算法(Radix-2 FFT)是最广为人知的一种库利-图基快速傅立叶算法分支。此方法不断地将N点的FFT拆解成两个'N/2'点的FFT,利用旋转因子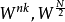 的对称性借此来降低DFT的计算复杂度,达到加速的功效。
的对称性借此来降低DFT的计算复杂度,达到加速的功效。
而其实前述有关时域抽取或是频域抽取的方法介绍,即为2基底的快速傅立叶转换法。以下展示其他种2基底快速傅立叶算法的连线方法,此种不规则的连线方法可以让输出与输入都为循序排列,但是连线的复杂度却大大的增加。
4基底4基底快速傅立叶变换算法则是承接2基底的概念,在此里用时域抽取的技巧,将原本的DFT公式拆解为四个一组的形式:
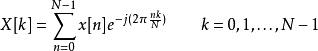

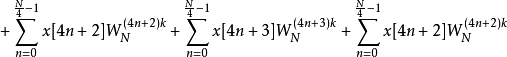
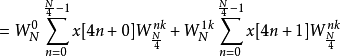
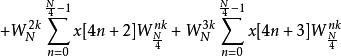

在这里再利用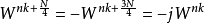 的特性来进行与2基数FFT类似的化减方法,以降低算法复杂度。
的特性来进行与2基数FFT类似的化减方法,以降低算法复杂度。
8基底在库利-图基算法里,使用的基底(radix)越大,复数的乘法与存储器的访问就越少,所带来的好处不言而喻。但是随之而来的就是实数的乘法与实数的加法也会增加,尤其计算单元的设计也就越复杂,对于可应用FFT之点数限制也就越严格。在表中我们可以看到在不同基底下所需的计算成本。
|| ||
在DFT的公式中,我们重新定义x=[x(0),x(1),…,x(N-1)]T, X=[X(0),X(1),…,X(N-1)]T,则DFT可重写为X=FN‧x。FN是一个N×N的DFT矩阵,其元素定义为[FN]ij=WNij(i,j ∈ [0,N-1]),当N=8时,我们可以得到以下的F8矩阵并且进一步将其拆解。
在拆解成三个矩阵相乘之后,我们可以将复数运算的数量从56个降至24个复数的加法。底下是8基底的的SFG。要注意的是所有的输出与输入都是复数的形式,而输出与输入的排序也并非规律排列,此种排列方式是为了要达到接线的最优化。

混合基底2-8基底在2/8基底的算法中,我们可以看到我们对于偶数项的输出会使用2基底的分解法,对于奇数项的输出采用8基底的分解法。这个做法充分利用了2基底与4基底拥有最少乘法数与加法数的特性。当使用了2基底的分解法后,偶数项的输出如下所示。
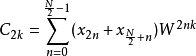 奇数项的输出则交由8基底分解来处理,如下四式所述。
奇数项的输出则交由8基底分解来处理,如下四式所述。

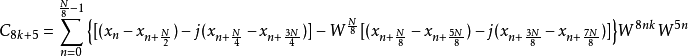
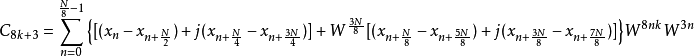
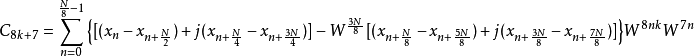
以上式子就是2/8基底的FFT快速算法。在架构图上可化为L型的蝴蝶运算架构,如下图所示。
2-4-8基底为了改进Radix 2/8在架构上的不规则性,我们在这里做了一些修改,如下表.。此修改可让架构更加规则,且所使用的加法器与乘法器数量更加减少,如下表所示。
|| ||
在这里我们最小的运算单元称为PE(Process Element),PE内部包含了2/8基底、2/4基底、2基底的运算,简化过的信号处理流程与蝴蝶型架构图可见下图
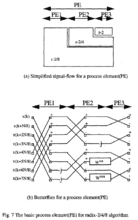
4基底基底的选择越大会造成蝴蝶形架构更加复杂,控制电路也会复杂化。因此Shousheng He和Mats Torkelson在1996提出了一个2^2基底的FFT算法,利用旋转因子的特性: 。而–j的乘法基本上只需要将被乘数的实部虚部对调,然后将虚部加上负号即可,这样的负数乘法被定义为'简单乘法',因此可以用很简单的硬件架构来实现。利用上面的特性,22基底FFT能用串接的方式将旋转因子以4为单位对DFT公式进行拆解,将蝴蝶形架构层数降到log4N,大幅减少复数乘法器的用量,而同时却维持了2基底蝴蝶形架构的简单性,在性能上获得改进。2^2基底DIF FFT算法的拆解方法如下列公式所述:
。而–j的乘法基本上只需要将被乘数的实部虚部对调,然后将虚部加上负号即可,这样的负数乘法被定义为'简单乘法',因此可以用很简单的硬件架构来实现。利用上面的特性,22基底FFT能用串接的方式将旋转因子以4为单位对DFT公式进行拆解,将蝴蝶形架构层数降到log4N,大幅减少复数乘法器的用量,而同时却维持了2基底蝴蝶形架构的简单性,在性能上获得改进。2^2基底DIF FFT算法的拆解方法如下列公式所述:
N点DFT公式:
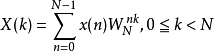
利用线性映射将n与k映射到三个维度上面

然后套用Common Factor Algorithm(CFA)
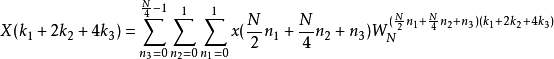
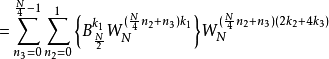
而蝴蝶型架构会变成以下形式
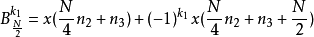 利用旋转因子
利用旋转因子 的特性,可以观察出
的特性,可以观察出
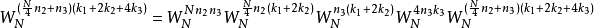
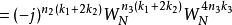 再将此公式带入原式中可以得到
再将此公式带入原式中可以得到
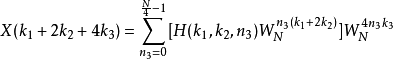
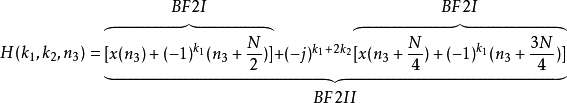
如上述公式所示,原本的DFT公式会被拆解成多个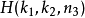 ,而
,而 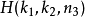 又可分为BF2I与BF2II两个层次结构,分别会对应到之后所介绍的两种硬件架构。
又可分为BF2I与BF2II两个层次结构,分别会对应到之后所介绍的两种硬件架构。
一个16点的DFT公式经过一次上面所述之拆解之后可得下面的FFT架构

可以看出上图的架构保留了2基底的简单架构,然而复数乘法却降到每两级才出现一次,也就是 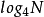 次。而BF2I以及BF2II所对应的硬件架构下图:
次。而BF2I以及BF2II所对应的硬件架构下图:
其中BF2II硬件单元中左下角的交叉电路就是用来处理-j的乘法。
一个256点的FFT架构可以由下面的硬件来实现:
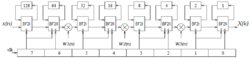
其中图下方的为一7比特宽的计数器,而此架构的控制电路相当单纯,只要将计数器的各个比特分别接上BF2I与BF2II单元即可。
下表将2基底、4基底与22基底算法做一比较,可以发现22基底算法所需要的乘法气数量为2基底的一半,加法弃用量是4基底的一半,并维持一样的存储器用量和控制电路的简单性。
|| ||
8基底如上所述,22算法是将旋转因子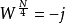 视为一个简单乘法,进而由公式以及硬件上的化简获得硬件需求上的改进。而借由相同的概念,Shousheng He和Mats Torkelson进一步将旋转因子
视为一个简单乘法,进而由公式以及硬件上的化简获得硬件需求上的改进。而借由相同的概念,Shousheng He和Mats Torkelson进一步将旋转因子  的乘法化简成一个简单乘法,而化简的方法将会在下面讲解。
的乘法化简成一个简单乘法,而化简的方法将会在下面讲解。
在2基数FFT算法中的基本概念是利用旋转因子 的对称性,4基数算法则是利用
的对称性,4基数算法则是利用  的特性。但是我们会发在这些旋转因子的对称特性中出现。
的特性。但是我们会发在这些旋转因子的对称特性中出现。
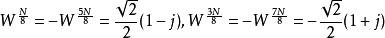
─并没有被利用到。主要是因为 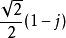 的乘法运算会让整个FFT变得复杂,但是如果借由近似的方法,我们便可以将此一运算化简为12个加法。
的乘法运算会让整个FFT变得复杂,但是如果借由近似的方法,我们便可以将此一运算化简为12个加法。
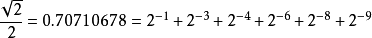 我们可以从上式注意到,
我们可以从上式注意到, 可以被近似为五个加法的结果,所以
可以被近似为五个加法的结果,所以 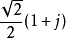 就可以被简化为只有六个加法,再算入实部与虚部的计算,总共只需12个加法器就可以运用到此一简化特性。
就可以被简化为只有六个加法,再算入实部与虚部的计算,总共只需12个加法器就可以运用到此一简化特性。
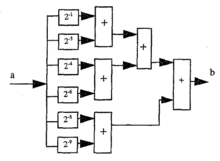
经由与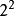 基底类似的推导,并用串接的方式将旋转因子以8为单位对DFT公式进行拆解,
基底类似的推导,并用串接的方式将旋转因子以8为单位对DFT公式进行拆解,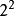 基底FFT算法进一步将复数乘法器的用量缩减到log8N,并同时维持硬件架构的简单性。推导的方法与
基底FFT算法进一步将复数乘法器的用量缩减到log8N,并同时维持硬件架构的简单性。推导的方法与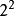 基底相当类似。借由这样的方法,
基底相当类似。借由这样的方法,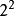 基底能将乘法器的用量缩减到2基底的1/3,并同时维持一样的存储器用量以及控制电路的简单性。
基底能将乘法器的用量缩减到2基底的1/3,并同时维持一样的存储器用量以及控制电路的简单性。
本词条内容贡献者为:
孔祥杰 - 副教授 - 大连理工大学软件学院