卡塔朗数

卡塔朗数(Catalan number)是一个组合数，一些组合计数问题可以归结为解下列形式的递归关系：un=u1un-1+u2un-2+…+un-1u1，n≥2，且u1=1，它的解un称为卡塔朗数1。一般认为这种数是由比利时数学家卡塔朗(E.C.Catalan，1814-1894)在1838年首先提出的，但后来有人指出，实际上大数学家欧拉早在1758年就已认识到它了。我国内蒙古师范大学罗见今副教授以大量的史料论证，所谓“卡塔朗数”的首创者其实并非欧洲人，而是我国清朝的蒙古族学者明安图(1692～1763)。他的发现早于欧拉，比卡塔朗的发现，几乎早了一百年2。

基本介绍卡塔朗数是一个组合数，一些组合计数问题可以归结为解下列形式的递归关系：un=u1un-1+u2un-2+…+un-1u1，n≥2，且u1=1，它的解为

un称为卡塔朗数，它的生成函数是

解下列这类问题都能得到卡塔朗数1：

1.把一个凸n+1边形用n-2条对角线将它分成互不重叠的三角形，这种分法的总数为un；

2.用n条互不相交的弦连结圆周上2n个点的不同方式总数为un+1；

3.有n个端点(根点除外)的3阶平面植树的个数为un；

4.n个元a1，a2，…，an不改变顺序组成连乘积，可以用n-1个括号表示相乘的过程，所有不同过程的个数是un；

5.坐标平面上由O(0，0)至点U(2n，0)的路径，每段由格点(i，j)至(i+1，j+1)或(i+1，j-1)，所有在上半平面内且允许经过x轴上的点、而不许越过x轴的路径数等于un+1；

6.由O(0，0)至U(2n，0)的路径，但不允许中间经过x轴上的点，共有un条。

卡塔朗数的前几项如下1：

u1=1， u2=1， u3=2， u4=5， u5=14，

u6=42， u7=132， u8=429，

u9=1430， u10=4862。

相关分析公园售票窗口前有2n个人排队买票，每张门票定价5角，每人限购一张。这些人中，只带一张5角人民币的与只带一张1元人民币的各有n人。开始售票时，售票窗口没有角票可以找零。试问：大家都能顺利买票，售票员始终没有找不出零钱困扰的排队方法共有多少种2?

用0代表身边带5角钱的人，1代表带1元钱的人，则本问题即可变成：有n个0和n个1，问有多少种排列方法，使排成的0、1序列里，任意前i(i可从1变到2n)个数字中，0的个数总不少于1的个数，此性质称为前束性质。如能将问题转化为图形，那当然更易了解。为此，我们把0看作向右走一步，把1看作向上走一步，则很明显，n个0和n个1所组成的序列将和图中从原点(0，0)到点(n，n)的递增路径是一一对应的。于是，我们只要计算路径的条数就行了。

再进一步看问题，具有前束性质的0、1序列正好与不越过对角线OA的递增路径一一对应(见图1)。而这种路径的条数

其中(n=0，1，2，…)，这就是有名的卡塔朗数，其前十项是1，1，2，5，14，42，132，429，1430，4862。

除了排队找零票问题可以引出卡塔朗数之外，凸n+1边形的三角形剖分方法种数(如图2，这种三角形只能以凸多边形的边与对角线为其三边)以及n个指定了顺序的实数的乘积结合方式种数也都可以引出它。据不完全统计，卡塔朗数的各种组合数学的解释已经不下五十种之多。

卡塔朗数还有一个极其直观的几何意义，它可以看作是杨辉三角形中“中垂线”上的数除以依次递增的自然数而得见图3)2。

卡塔朗数有一个简单而漂亮的递推公式如下：

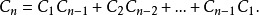
本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学