科技工作者之家
科技工作者之家APP是专注科技人才,知识分享与人才交流的服务平台。
科技工作者之家 2020-11-17
可表示拟阵(representable matroid)亦称可坐标化拟阵,是一种组合构形,它是与有限域GF(q)上的矩阵拟阵M(A)有一一对应关系的拟阵M(E),称M(A)为拟阵M(E)的表示,矩阵A为拟阵的表示矩阵1。
基本介绍定义1 设M是个拟阵,若存在某个域F,及域F上的一个矩阵A使得M MF[A],则称M是个F-**可线性表示拟阵(F-representable matroid),或(在不强调F的时候)称M为一个可线性表示拟阵**(representable matroid)(也常简称为F-可表示拟阵或可表示拟阵);而矩阵A则称为M的一个F-线性表示(F-representation)(或简称为F-表示),有时也称A为M在F上的一个坐标****化(F-coordinatization)。若存在某个图G,使得M
MF[A],则称M是个F-**可线性表示拟阵(F-representable matroid),或(在不强调F的时候)称M为一个可线性表示拟阵**(representable matroid)(也常简称为F-可表示拟阵或可表示拟阵);而矩阵A则称为M的一个F-线性表示(F-representation)(或简称为F-表示),有时也称A为M在F上的一个坐标****化(F-coordinatization)。若存在某个图G,使得M M(G),则称M为可图拟阵(graphicmatroid)。
M(G),则称M为可图拟阵(graphicmatroid)。
例如,在完全图K4上的图拟阵M(K4)在二元域GF(2)上是可表示的;但是,均匀拟阵U2,4在二元域GF(2)上却是不可表示的,尽管它在其他域上是可表示的(见下图和下表)。可表示拟阵的对偶拟阵、子拟阵亦均为可表示的。这是可表示拟阵的优越性所在。


特别地,把能够在二元域GF(2)上表示的拟阵称为二元拟阵。均匀拟阵U2,3为二元拟阵。因为对于三元素集E={a,b,c},其任意真子集都是U2,3的独立集,而E为相关集。相应的表示向量为α(a)=(1,0),α(b)=(0,1),α(c)=(1,1)。均匀拟阵U2,4却不是二元拟阵。二元拟阵包含了单模拟阵和图拟阵等重要拟阵。在拟阵的表示理论中,二元拟阵是研究较早的一类1。
相关介绍定义2对于给定的两个拟阵M₁(Z₁,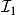 )和M₂(Z₂,
)和M₂(Z₂, ),若映射
),若映射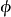 :E₁→E₂满足以下的条件:
:E₁→E₂满足以下的条件:
(i) :E₁→E₂是一个一一对应,
:E₁→E₂是一个一一对应,
(ii)对任意子集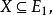 X∈
X∈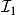 当且仅当
当且仅当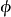 (X)∈
(X)∈ ,
,
则称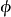 :E₁→E₂为从M₁到M₂的一个同构。若这样的
:E₁→E₂为从M₁到M₂的一个同构。若这样的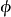 存在,称M₁与M₂同构,记作M₁
存在,称M₁与M₂同构,记作M₁ M₂。对每个拟阵M,易见全体从M到M的同构在映射的复合下构成一个群Aut(M)(称为M的自同构群)。
M₂。对每个拟阵M,易见全体从M到M的同构在映射的复合下构成一个群Aut(M)(称为M的自同构群)。
作为例子,如下(1),(2),若且是(1)中的矩阵而G是(2)中的图,则M[A] (M(G),其同构映射就是
(M(G),其同构映射就是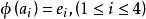 。
。
(1)考虑实数域R上的矩阵
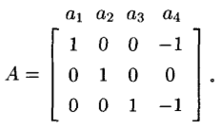
令ai(1≤i≤4)代表A的第i个列向量的标号i,又令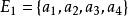 为A的列向量的标号集合。要确定所有独立集的集族
为A的列向量的标号集合。要确定所有独立集的集族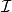 ,我们要找出所有的子集I⊆E1,使得由I中元素所标号的向量组在V(3,R)中线性无关。从线性代数中我们知道,任何一个线性无关向量组都被一个极大线性无关向量组所包含。因此我们只要找出A的列向量中的全体极大线性无关向量组。不难看出,A的全体极大线性无关向量组由E1的这些子集所标号
,我们要找出所有的子集I⊆E1,使得由I中元素所标号的向量组在V(3,R)中线性无关。从线性代数中我们知道,任何一个线性无关向量组都被一个极大线性无关向量组所包含。因此我们只要找出A的列向量中的全体极大线性无关向量组。不难看出,A的全体极大线性无关向量组由E1的这些子集所标号
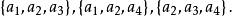 因此
因此
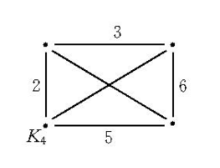
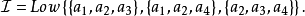 (2)考虑图G
(2)考虑图G
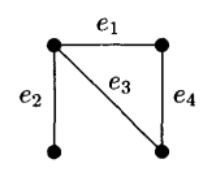
其边集为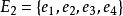 。我们要确定所有无圈子图的边集的集族
。我们要确定所有无圈子图的边集的集族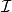 。由于每一个无圈子图都是一个支撑树的子图,因此我们只要找出G的所有的支撑树。不难看出G的全体支撑树对应的边子集是
。由于每一个无圈子图都是一个支撑树的子图,因此我们只要找出G的所有的支撑树。不难看出G的全体支撑树对应的边子集是
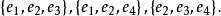 因此,
因此,
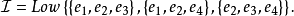
进一步的观察可以看出,(1)与(2)这两个例子,除了一个从矩阵出发得到,另一个从图得到以外,它们有互相对应的独立子集族,因而它们的独立结构没有什么本质的区别,为此我们有同构的定义2。
本词条内容贡献者为:
任毅如 - 副教授 - 湖南大学