科技工作者之家
科技工作者之家APP是专注科技人才,知识分享与人才交流的服务平台。
科技工作者之家 2020-11-17
互质因子算法(Prime-factor FFT algorithm, PFA),又称为Good-Thomas算法,是一种快速傅立叶变换(FFT),把N = N1N2大小的离散傅立叶变换重新表示为N1*N2大小的二维离散傅立叶变换,其中N1与N2需互质。变成N1和N2大小的傅立叶变换后,可以继续递回使用PFA,或用其他快速傅立叶变换算法来计算。
简介较流行的Cooley-Tukey算法经由mixed-radix一般化后,也是把N = N1N2大小的离散傅立叶变换分割为N1和N2大小的转换,但和互质因子算法 (PFA)作法并不相同,不应混淆。Cooley-Tukey算法的N1与N2不需互质,可以是任何整数。然而有个缺点是比PFA多出一些乘法,和单位根twiddle factors相乘。相对的,PFA的缺点则是N1与N2需互质 (例如N 是2次方就不适用),而且要借由中国剩余定理来进行较复杂的re-indexing。互质因子算法 (PFA)可以和mixed-radix Cooley-Tukey算法相结合,前者将N 分解为互质的因数,后者则用在重复质因数上。
PFA也与nested Winograd FFT算法密切相关,后者使用更为精巧的二维折积技巧分解成N1 * N2的转换。因而一些较古老的论文把Winograd算法称为PFA FFT。
尽管PFA和Cooley-Tukey算法并不相同,但有趣的是Cooley和Tukey在他们1965年发表的有名的论文中,没有发觉到高斯和其他人更早的研究,只引用Good在1958年发表的PFA作为前人的FFT结果。刚开始的时候人们对这两种作法是否不同有点困惑。1
算法离散傅立叶变换(DFT)的定义如下:
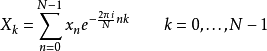
PFA将输入和输出re-indexing,代入DFT公式后转换成二维DFT。
Re-indexing设N = N1N2,N1与N2两者互质,然后把输入n 和输出k 一一对应到
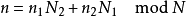
因N1与N2 互质,故根据最大公因数表现定理,对每个n 都存在满足上式的整数n1与n2,且在同余N 之下n1可以调整至0~N1 –1之间,n2可以调整至0~N2 –1之间。并根据同余理论易知满足上式且在以上范围内的整数n1与n2是只有一个的。这称为Ruritanian 映射 (或Good's 映射),
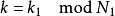
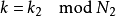
举例来说:
如果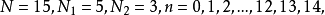 对于任一
对于任一 都可以对应到
都可以对应到
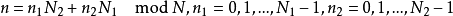
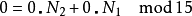
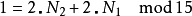
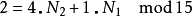
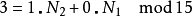
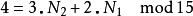
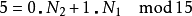
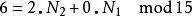
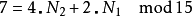
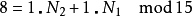
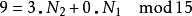
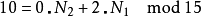
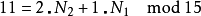
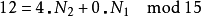
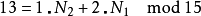
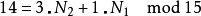
因N1与N2互质,故根据中国剩余定理,对于每组 (k1,k2) (其中k1在0~N1– 1之间,k2在0~N2– 1之间),都有存在且只有一个的k在0~N- 1之间且满足上两式。这称为CRT映射。CRT映射的另一种表示法如下
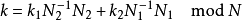
其中N1表示N1在模N2之下的反元素,N2反之。
( 也可以改成对输入n用CRT映射以及对输出k用Ruritanian映射)
对于有效re-indexing (理想上是达到原地)的方法有许多研究,以减少耗费时间的模运算。2
DFT re-expression表示方法一:
将以上的re-indexing代入DFT公式里指数部分的nk之中,
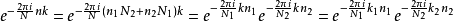
( 因为e= 1,所以两个指数的k部分可以分别模N1与N2)。剩下的部分变成
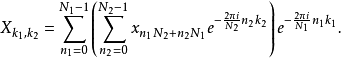
则内部和外部的总和分别转换成大小为N2与N1的DFT。
表示方法二:
如果令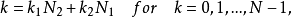
令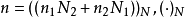 相当于取
相当于取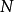 的余数,
的余数,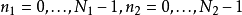
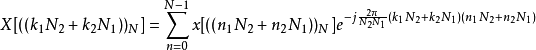
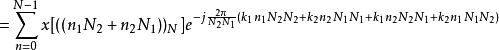
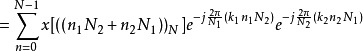
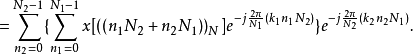
对于每一个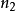 都要做一个
都要做一个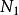 点的
点的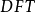 ,而因为
,而因为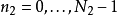 有
有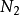 个,所以需要
个,所以需要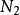 个
个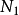 点
点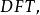
对于每一组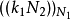 都要做一个
都要做一个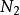 点的
点的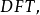 而因为
而因为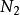 为常数,
为常数,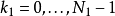 有
有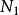 个,所以需要
个,所以需要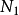 个
个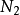 点
点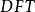 ,
,
因此如果要计算复杂度,可以乘法器的数量当作考量,
假设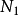 点的
点的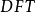 需要
需要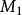 个乘法器,
个乘法器,
假设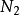 点的
点的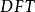 需要
需要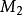 个乘法器,
个乘法器,
则总共需要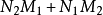 个乘法器。
个乘法器。
与Cooley-Tukey算法的比较如首段所述,Cooley-Tukey算法和互质因子算法 (PFA)曾被误认为很类似。两者皆有各自优点可适用于不同状况,因此分辨它们的不同是很重要的。在1965年著名的论文中发表的Cooley-Tukey算法,是在DFT的定义
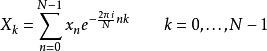
中代入n=n1+n2N1,k=k1N2+k2,则
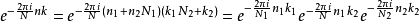
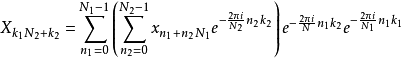
比PFA多了一些要乘的因子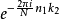 (称为twiddle factors),但index较为简单,且适用于任何N1、N2。在J. Cooley稍后发表的关于FFT历史探讨的论文中使用N= 24点FFT为例,显示两种作法在index结构上的不同。
(称为twiddle factors),但index较为简单,且适用于任何N1、N2。在J. Cooley稍后发表的关于FFT历史探讨的论文中使用N= 24点FFT为例,显示两种作法在index结构上的不同。
本词条内容贡献者为:
何星 - 副教授 - 上海交通大学