圆内接折四边形

圆内接折四边形(inscribed broken quadrilateral in a circle)是与圆相关的一个折四边形，折四边形是指有一组对边相交的复杂四边形，圆内接折四边形就是指四个顶点在同一圆上的折四边形。

基本介绍圆内接折四边形是与圆相关的一个折四边形，指四个顶点在同一圆上的折四边形。此圆称为折四边形的外接圆。

圆内接折四边形判定定理：如果折四边形的一组对角相等，那么这个折四边形内接于圆。

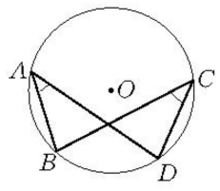
如图1，折四边形ABCD中，一组对角∠A=∠C，那么折四边形内接于一个圆。

反之，圆内接折四边形性质定理：圆内接折四边形的两组对角都相等。

如图1，折四边形ABCD内接于⊙O，那么∠A=∠C，∠B=∠D1。

圆内接四边形圆内接四边形(inscribed quadrilateral)是具有四条边的圆内接多边形。圆内接四边形或为凸四边形或为折四边形，若为前者，其对角互补；任一外角等于其内对角，如图2。若为后者，其对角相等。上述两者其逆命题均成立，它们均是证明四点共圆的主要定理2。

|| ||

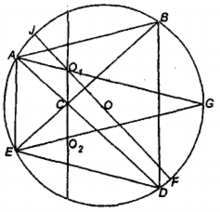
圆内接四边形相关结论命题1 设⊙O的圆心，半径分别为O、R。ABCDE是⊙O的任一内折四边形(C是折点)。记△CAB、△CDE分别是△₁、△₂。再记： 分别是△i的内心、内切圆半径，且 ，则3

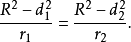
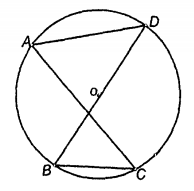
命题2 设⊙O的圆心、半径分别为O、R。ABCD是⊙O的任一内接四边形。若记△ABC、△ABD分别为△₁、△₂。再记 分别是△i的内心、内切圆半径，且，则有

引用察柏尔(chapple)定理，可以获得下面结论3。

命题3记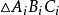的外心、内心、外接圆半径、内切圆半径分别为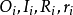，且，则有

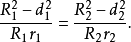
察柏尔定理：若△ABC的外接圆半径、内切圆半径分别为R、r，而△ABC的内、外心距为d，则R²-d²=2Rr。

命题4 设⊙O的圆心、半径分别为O、R。ABCDE是⊙O的任一内折四边形(C是折点)。记△CAB、△CDE分别是△₁、△₂；再记：分别是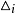的内心、内切圆半径、外接圆半径，且，则有

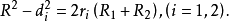
注1 本命题的结果很容易得到：。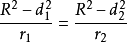

注2 若考虑本命题讨论图形的以下极端情况：△CDE退缩为一点，△CAB胀至内接⊙O，则有R²-d²=2Rr(r、R分别为△ABC的内切圆半径和外接圆半径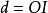；，是△ABC的内心)。此便是察柏尔定理3。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学