科技工作者之家
科技工作者之家APP是专注科技人才,知识分享与人才交流的服务平台。
科技工作者之家 2020-11-17
在计算机科学中,布尔可满足性问题(有时称为命题可满足性问题,缩写为SATISFIABILITY或SAT)是确定是否存在满足给定布尔公式的解释的问题。换句话说,它询问给定布尔公式的变量是否可以一致地用值TRUE或FALSE替换,公式计算结果为TRUE。如果是这种情况,公式称为可满足。另一方面,如果不存在这样的赋值,则对于所有可能的变量赋值,公式表示的函数为FALSE,并且公式不可满足。例如,公式“a AND NOT b”是可以满足的,因为可以找到值a = TRUE且b = FALSE,这使得(a AND NOT b)= TRUE。相反,“a AND NOT a”是不可满足的。
基本定义和术语命题逻辑公式,也称为布尔表达式,由变量,运算符AND(连接,也用∧表示),OR(分离,∨), NOT (否定,¬)和括号构成。如果通过为其变量分配适当的逻辑值(即TRUE,FALSE)可以使公式为TRUE,则称该公式是可满足的。给定公式,布尔可满足性问题(SAT)是检查它是否可满足。这个决策问题在计算机科学的各个领域都至关重要,包括理论计算机科学,复杂性理论,算法,密码学和人工智能。
布尔可满足性问题有几种特殊情况,其中公式需要具有特定结构。文字是一个变量,称为正文字,或变量的否定,称为负文字。子句是文字(或单个文字)的分离。如果一个子句最多包含一个正文字,则该子句称为Horn子句。如果公式是条款(或单个子句)的连接,则公式为合取范式(CNF)。例如,x1是正文字,¬x2是负文字,x1∨¬x2是子句,(x1∨¬x2)∧(¬x1∨x2∨x3)∧×x1是联合范式的公式;它的第一和第三个条款是Horn条款,但它的第二个条款不是。公式是可以满足的,通过选择x1 = FALSE,x2 = FALSE和x3任意,因为(FALSE∨FALSE)∧(¬FALSE∨FALSE∨3)∧FALSE求值为(FALSE∨TRUE)∧(TRUE∨FALSE ∨x3)∧TRUE,依次为TRUE∧TRUE∧TRUE(即为TRUE)。相反,CNF公式a∧¬a由一个文字的两个子句组成,是不可满足的,因为对于a = TRUE或a = FALSE,它评估为TRUE∧TRUE(即FALSE)或FALSE∧FALSE(即,分别为FALSE)。
对于SAT问题的某些版本,定义广义联合范式公式的概念是有用的,即。作为任意多个广义子句的连接,后者对于某些布尔运算符R和(普通)文字li具有R(l1,...,ln)形式。不同的允许布尔运算符集导致不同的问题版本。例如,R(¬x,a,b)是一个广义子句,R(¬x,a,b)∧R(b,y,c)∧ R(c,d,¬z)是广义的联合正规形式。下面使用此公式,其中R是三元运算符,只有当其中一个参数为时才为TRUE。
使用布尔代数的定律,每个命题逻辑公式都可以转换为等效的连接法线形式,然而,它可以指数地更长。例如,将公式(x1∧y1)∨(x2∧y2)∨...∨(xn∧yn)转换为连接法线形式。
(x1∨x2∨…∨xn) ∧
(y1∨x2∨…∨xn) ∧
(x1∨y2∨…∨xn) ∧
(y1∨y2∨…∨xn) ∧ ... ∧
(x1∨x2∨…∨yn) ∧
(y1∨x2∨…∨yn) ∧
(x1∨y2∨…∨yn) ∧
(y1∨y2∨…∨yn);
而前者是2个变量的n个连接的分离,后者由n个变量的2n个子句组成。
复杂性和受限制的版本无限制的可满足性SAT是第一个已知的NP完全问题,1971年多伦多大学的Stephen Cook [2]和1973年国家科学院的Leonid Levin独立证明了这一问题。在此之前,NP完全问题的概念甚至不存在。证明显示复杂性类NP中的每个决策问题如何可以简化为CNF公式的SAT问题,有时称为CNFSAT。 Cook减少的一个有用特性是它保留了接受答案的数量。例如,确定给定图形是否具有3色是NP中的另一个问题;如果一个图表有17个有效的3色,那么Cook-Levin减少产生的SAT公式将有17个令人满意的分配。
NP完全性仅指最坏情况实例的运行时间。实际应用中出现的许多实例可以更快地解决。请参阅下面的解算SAT的算法。
如果公式仅限于析取正规形式,即它们是文字连词的脱节,那么SAT是微不足道的。当且仅当其连接中的至少一个是可满足的时,这样的公式确实是可满足的,并且当且仅当它对于某个变量x不包含x和NOT x时,连接是可满足的。这可以在线性时间内检查。此外,如果它们被限制为完全分离正常形式,其中每个变量在每个连接中恰好出现一次,则可以在恒定时间内检查它们(每个连接代表一个令人满意的分配)。但是,将一般SAT问题转换为析取范式可能需要指数时间和空间;例如,对于联合正规形式,在上述指数爆炸示例中交换“∧”和“∨”。
3-可满足性与任意公式的可满足性问题一样,确定公式的可满足性,其中每个条款限制为最多三个文字的连续正规形式也是NP完全的; 这个问题被称为3-SAT,3CNFSAT或3-satisfiability。为了将无限制的SAT问题减少到3-SAT,将每个子句l1∨⋯∨ln转换为n-2个子句的连接。
(l1 ∨ l2 ∨ x2) ∧
(¬x2 ∨ l3 ∨ x3) ∧
(¬x3 ∨ l4 ∨ x4) ∧ ⋯ ∧
(¬xn− 3 ∨ ln− 2 ∨ xn− 2) ∧
(¬xn− 2 ∨ ln− 1 ∨ ln)
其中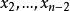 是其他地方没有出现的新变量。虽然这两个公式在逻辑上不相同,但它们是完全可以满足的。转换所有子句得到的公式最多是其原始的3倍,即长度增长是多项式的。
是其他地方没有出现的新变量。虽然这两个公式在逻辑上不相同,但它们是完全可以满足的。转换所有子句得到的公式最多是其原始的3倍,即长度增长是多项式的。
3-SAT是卡普的21个NP完全问题之一,它被用作证明其他问题也是NP难的起点。这是通过从3-SAT到3-SAT的多项式时间减少来完成的。其他问题。使用此方法的问题的一个例子是clique问题:给定由c子句组成的CNF公式,相应的图由每个文字的顶点和每两个非矛盾文字之间的边组成来自不同的条款,参见图片。当且仅当公式可满足时,该图具有c-clique。
Schöning(1999)有一个简单的随机算法,该算法在时间(4/3)n中运行,其中n是3-SAT命题中的变量数,并且很有可能成功地正确决定3-SAT。
指数时间假设断言在exp(o(n))时间内没有算法可以解决3-SAT(或者实际上任何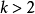 的k-SAT)(即,基本上比n中的指数更快)。
的k-SAT)(即,基本上比n中的指数更快)。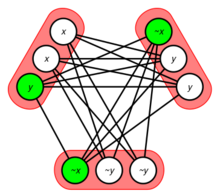
Selman,Mitchell和Levesque(1996)给出了随机生成的3-SAT公式难度的经验数据,具体取决于它们的大小参数。难度是通过DPLL算法进行的数量递归调用来衡量的。
当考虑CNF中的公式时,3个可满足性可以推广到k-可满足性(k-SAT,也就是k-CNF-SAT),每个子句包含多达k个文字。然而,因为对于任何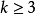 ,这个问题既不比3-SAT更容易也不比SAT更难,后两者是NP完全的,所以必须是k-SAT。
,这个问题既不比3-SAT更容易也不比SAT更难,后两者是NP完全的,所以必须是k-SAT。
一些作者将k-SAT限制为具有k个文字的CNF公式。这也不会导致不同的复杂性类,因为每个子句l1∨⋯∨lj与j