皮卡小定理

皮卡定理是两个不同的数学定理的泛称，由法国数学家埃米尔·皮卡证明。这两个定理都涉及解析函数的值域。皮卡小定理说明，如果函数f(z)是整函数且不是常数，则f(z)的值域或者是整个复平面，或者只去掉一个点。 这个定理在1879年证明。它强化了刘维尔定理：任何不是常数的整函数都一定是无界的。

简介皮卡定理是两个不同的数学定理的泛称，由法国数学家埃米尔·皮卡证明。这两个定理都涉及解析函数的值域。皮卡小定理说明，如果函数f(z)是整函数且不是常数，则f(z)的值域或者是整个复平面，或者只去掉一个点。 这个定理在1879年证明。它强化了刘维尔定理：任何不是常数的整函数都一定是无界的。1

定理的表述小定理皮卡小定理说明，如果函数f(z)是整函数且不是常数，则f(z)的值域或者是整个复平面，或者只去掉一个点。 这个定理在1879年证明。它强化了刘维尔定理：任何不是常数的整函数都一定是无界的。

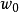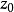皮卡的原始证明利用了模函数（Modular lambda function）。证明概要如下：若f(z)的值域不包含复平面上的两个点，不失一般性地，可以假设f(z)的值域不包含0和1，设是其值域中的点，在这个点附近，可以选取模函数的逆的某个单值解析分支，记作。利用模函数的通用覆盖性和单值性定理，可以将点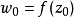（）附近定义的复合映射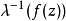解析延拓到整个复平面上，从而得到一个在复平面上单值解析但有界的函数。根据刘维尔定理，该函数为常函数。因此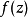也是常函数。

大定理皮卡大定理说明，如果f(z)在点w具有本性奇点，那么在任何含有w的开集中，f(z)都将取得所有可能的复数值，最多只有一个例外。

这个定理强化了魏尔施特拉斯-卡索拉蒂定理，它只保证了f的值域在复平面内是稠密的。1

评论这个“唯一的例外”实际上在两个定理中都是需要的：指数函数e是一个整函数，永远不能是零。e在0处具有本性奇点，但仍然不能取得零。

皮卡大定理在一个更一般的形式中也是正确的，可以应用于亚纯函数：如果M是一个黎曼曲面，w是M上的一个点，P****C=C∪{∞}表示黎曼球面，f:M\{w}→P****C是一个全纯函数，在w处具有本性奇点，那么在M的任何含有w的开子集中，函数f都可以取得除了两个点以外的所有P****C的点。

例如，亚纯函数f(z)=1/(1−exp(1/z))在z=0处具有本性奇点，在0的任何邻域内都无穷多次取得值∞；但它无法取得0或1的值。

皮卡小定理可以从皮卡大定理推出，因为整函数要么是多项式，要么在无穷远处具有本性奇点。1

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学