子布尔代数

子布尔代数(subalgebra of a Boolean algebra)是布尔代数的子代数，结构〈A，+A，·A，′A，0A，1A〉是布尔代数〈B，+B，·B，′B，0B，1B〉的子代数，是指A⊆B，0A=0B，1A=1B，运算+A，·A，′A是运算+B，·B，′B限制到A且A在运算+A，·A，′A下封闭。设B=〈B，+，·，′，0，1〉是布尔代数，S⊆B，B必有子代数，其论域包含S(例如B本身就是)，对B的一切其论域包含S的子代数作交集，可得B的子代数B0，称为其论域包含S的最小子布尔代数1。

基本介绍定理1 设(B，∨，∧，﹣，0，1)是一个布尔代数，S⊆B。如果S含有元素0和1，并且在运算∨、∧和﹣下封闭，则(S，∨，∧，﹣，0，1)是一个布尔代数2。

证明 由于S⊆B，0，1∈S且S在运算∨，∧和﹣下封闭，所以，如果a∈S，则∈S，于是Huntington公理中的(3)和(4)显然在S中成立；又交换律和分配律是继承的，所以(S，∨，∧，﹣，0，1)是一个布尔代数。

由此，有如下定义：

子布尔代数 设(B，∨，∧，﹣，0，1)是一个布尔代数，s⊆B。如果S含有元素0和1，并且在运算∨，∧和﹣下封闭，则称(S，∨，∧，﹣，0，1)是(B，∨，∧，﹣，0，1)的子布尔代数。

实际中，验证B的一个非空子集S是否是子布尔代数，不需要按定义进行，只须验证该子集对运算{∨，﹣}或{∧，﹣}封闭就可以了。这是因为若S≠∅且S对运算{∨，﹣}封闭，则存在a∈S，所以∈S，1=a∨∈S，0=∈S，且对∀a，b∈S，有

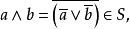故S是B的子布尔代数2。

例题解析例1 (1)对任何布尔代数(B，∨，∧，﹣，0，1)恒有子布尔代数(B，∨，∧，﹣，0，1)和({0，1}，∨，∧，﹣，0，1)，它们被称为(B，∨，∧，﹣，0，1)的平凡子布尔代数2。

(2)考察图1所示的布尔代数(B，∨，∧，﹣，0，1)。

1)S1={a，f，0，1}，S2={b，e，0，1}。由于S1、S2都含有0和1，且均对运算∨，∧和封闭，所以(S1，∨，∧，﹣，0，1)、(S2，∨，∧，﹣，0，1)均是(B，∨，∧，﹣，0，1)的子布尔代数。

2)S3={a，e，c，1}，S4={e，c，f，0}。由于S3不含0，S4不含1，所以它们都不是(B，∨，∧，﹣，0，1)的子布尔代数，但它们本身都构成布尔代数。

3)S5={a，c，0，1}对运算﹣不封闭(因为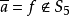)，所以S5不能构成(B，∨，∧，﹣，0，1)的子布尔代数2。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学