拟群

拟群(quasi-group)是一种代数系统。设集Q上有一个二元运算称为乘法，记为“°”，若对Q中任意元a，b，方程a°x=b及x°a=b在Q中都恰有一个解x，则称(Q，°)为一个拟群。当Q为有限集时，Q中元素个数称为拟群的阶，在n阶拟群(Q，°)的乘法表中，第a行第b列的元素为a°b，若记L=(mab)，mab=a°b，则由乘法表所得的阵列L是一个n阶拉丁方。反之，由一个n阶拉丁方作为乘法表所得的二元运算形成集Q上的一个拟群。若对拟群(Q，°)中的每个元x恒有x°x=x，则称该拟群是幂等的。若集Q上有n-2个n阶幂等拟群，使对Q中任意两个相异元a，b，集Q上n-2个值a°b取遍Q\{a，b}，则称这n-2个拟群构成一个幂等拟群大集。已知当n≥3且n≠6时，n阶幂等拟群大集总存在，而6阶幂等拟群大集则不可能存在1。

定义设集合Q的元素是a、b、c，...，如果定义了两个元素a、b的积，而且对于给定的a、c，存在唯一的b，使得ab=c，对于给定的b、c，存在唯一的a，使得ab=c，则称Q关于所定义的二元合成法则构成一个拟群2。

相关概念与性质1. 体的概念可以用一些彼此不等价的方法转移到非结合的情形上来。例如，可以考虑这样的环，在其中，对于任意元素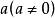和b，方程

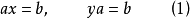有解，但解不一定是唯一确定的。我们将称任意这样的环为可除****环；从我们的定义可知，可除环可能有零因子。

一个可除环，如果在其中方程(1)的两方程各有唯一解，这样的可除环就叫作拟体。拟体不能包含零因子，因而拟体的非零元关于乘法组成群胚，这就是拟群，也就是一个群胚，在其中，对任意元素a和b，方程(1)的两方程均唯一可解。

最后，我们将把术语体留来专指有单位元的拟体。体的非零元素依乘法组成有单位元的拟群，也就是圈。

任意没有零因子的(不一定结合的)环可嵌入拟体中。

**2．**存在不是体的拟体和不是圈的拟群，问题在于虽然拟群G中对任意元素a方程

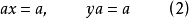唯一可解，但这些解不一定相同，且不一定分别是G中其他元素的右或左单位元。

有单位元e的圈G之任意子拟群A是子圈，并以原来的e为单位元。

这是因为，对任意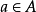，方程(2)在G内有唯一解e，因而它也含于子拟群A中。

**3．**关于群的一系列结果可推广到拟群，特别是可推广到圈上。对此我们不去作进一步的讨论，而只是引入同构的一个推广，它在拟群理论中起着显著的作用。

设给定一有乘法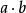的群胚G，井设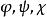是集G到自身上的任意一一映射，它们可以是相同的。若对任意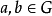，令

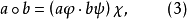则在集G上我们得到一个新的群胚。这个新群胚不一定与原来的同构，但在某种程度上它们是相近的。

与此相应地，有乘法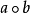的群胚G称为同形于有乘法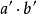的群胚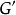，若存在G到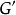上的三个一一映射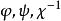，使得对任意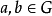，有

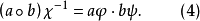显然，当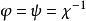时，我们便得G到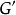上的同构映射。

易证，同形关系是自反的，传递的和对称的。

在许多情形，为了方便，将认为两运算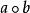和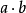是在同一集M上给定的，而且认为(3)或(4)中的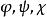是这个集到自身上的一一映射。

**4．**与拟群同形的任意群胚必是拟群。

事实上，设在集G上给定一有乘法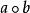的群胚和有乘法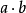的拟群，且知它们是同形的，也就是(3)成立。今证，例如，方程

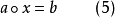对任意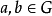有唯一解。我们知道，方程

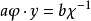有唯一确定的解c。令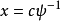，此时

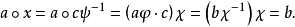另一方面，若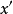是方程(5)的任一解，则

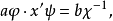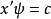从而，亦即。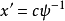

**5．**任意拟群同形于圈。

事实上，在有乘法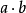的拟群G中固定任意一个元素e，此时在G中存在一元素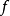，使

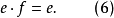
设a是G中任意元素，用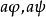表示由下面方程唯一确定的元素，

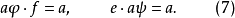
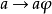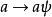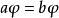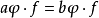映射和，是集G到自身上的一一映射，其中a遍经整个集G。譬如，若，则，亦即。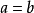

另一方面，若c是G中任一元素，则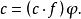

从而，对所有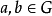，令

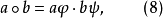则在G上我们定义了一个新群胚，它与原来的拟群同形；在这里恒等映射起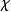的作用，有人把这叫作主向形。由上一款中证明过的知道，所得到的群胚是拟群，它还是圈，因为e是它的单位元。事实上，因为依(6)和(7)，

故依(8)和(7)，

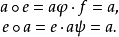定理证完3。

**6．**若有单位元的群胚同形于半群，则它们同构，因而两者都是结合的且两者都有单位元。

由此定理可得Albert定理：若圈同形于群，则它们同构。特别，由此推知同形的群永远同构，因此在群论中没有必要使用同形概念。

**7．**同形的概念也能转移到非结合环的理论中去。考察一些有同一加群G的环，和上面一样用等式(3)来定义环的同形，只是认定映射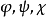是群G到自身上的同构映射，由上面得到的结果以及证明这些结果时利用的方法可以得出下面的一些结果：

同形于拟体的任意环本身也是拟体。

其他介绍在数学中，特别是抽象代数里，拟群是一种类似于群的代数结构。拟群与群的相像之处是也能够进行除法运算，但拟群中并没有群所拥有的结合律。有单位元的拟群称作幺拟群或者圈（loop）。

拟群的正规定义有两种，分别带有一种和三种二元运算。首先介绍第一种定义：

一个拟群 (Q, *) 是一个集合Q 与一个二元运算 * 的结合（即一个原群），满足对 Q 中的任意元素 a 和 b，都存在唯一的 Q 中元素 x 和 y，使得：

a*x = b ；

y*a = b 。

这两个唯一的元素被记作：x = a \ b 和 y = b / a。其中“\” 和 “/”分别表示被二元运算所定义的“左除法”和“右除法”。拟群的公理化需要用到存在量词，因此也就需要建立在一阶逻辑之上。

拟群的第二个定义是建立在泛代数的背景中。泛代数希望代数结构为簇，也就是说其公理化过程应该只需要到等式的概念。在这样的要求下，拟群被定义为：

一个拟群 (Q, *, \, /) 是一种 (2,2,2) 代数，其满足等式:

y = x * (x \ y) ；

y = x \ (x * y) ；

y = (y / x) * x ；

y = (y * x) / x 。

因此如果 (Q, *) 是依据第一种定义的拟群，那么 (Q, *, \, /) 则是其在泛代数范畴内对应的概念。

一个有单位元的拟群称为一个幺拟群或一个圈，这里的单位元是指 Q 中元素 e 使得：

x*e = x = e*x 。

可以证明单位元 e 是唯一的，并且这时每一个 Q 中元素都有唯一的一个左逆元和右逆元。

拉丁方一个有限拟群的乘法构成的乘法表是一个拉丁方：一个 n × n 的表格，每行每列都是 n 个不同的元素的排列，并且每个元素恰好出现在每一行和每一列各一次。

反之，每个拉丁方都可以以多种方式成为一个拟群的乘法表。

态射一个拟群或圈同态是两个拟群（圈）之间的映射：f : Q → P 满足 f(xy) = f(x)f(y)。 拟群同态保持了左右除法以及单位元（如果有的话）。

例子整数集合 Z 以及其上的减法 (−) 构成拟群（但不构成半群）。

所有非零的有理数的集合 Q* （或者所有非零实数构成的 R*）以及其上的除法 (÷) 构成一个拟群。

所有特征不为2的域上的向量空间以及其上的二元运算 x * y = (x + y) / 2 构成了一个幂等的交换的拟群。

每个斯坦纳三元系统都定义了一个幂等交换的拟群：其运算为将 a * b 对应到包含 a 和 b 的三元数组的第三个元。

非零八元数以及其上的乘法构成了一个圈，称为Moufang圈.

一般来说，一个可除代数上的所有非零元构成一个拟群。

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学